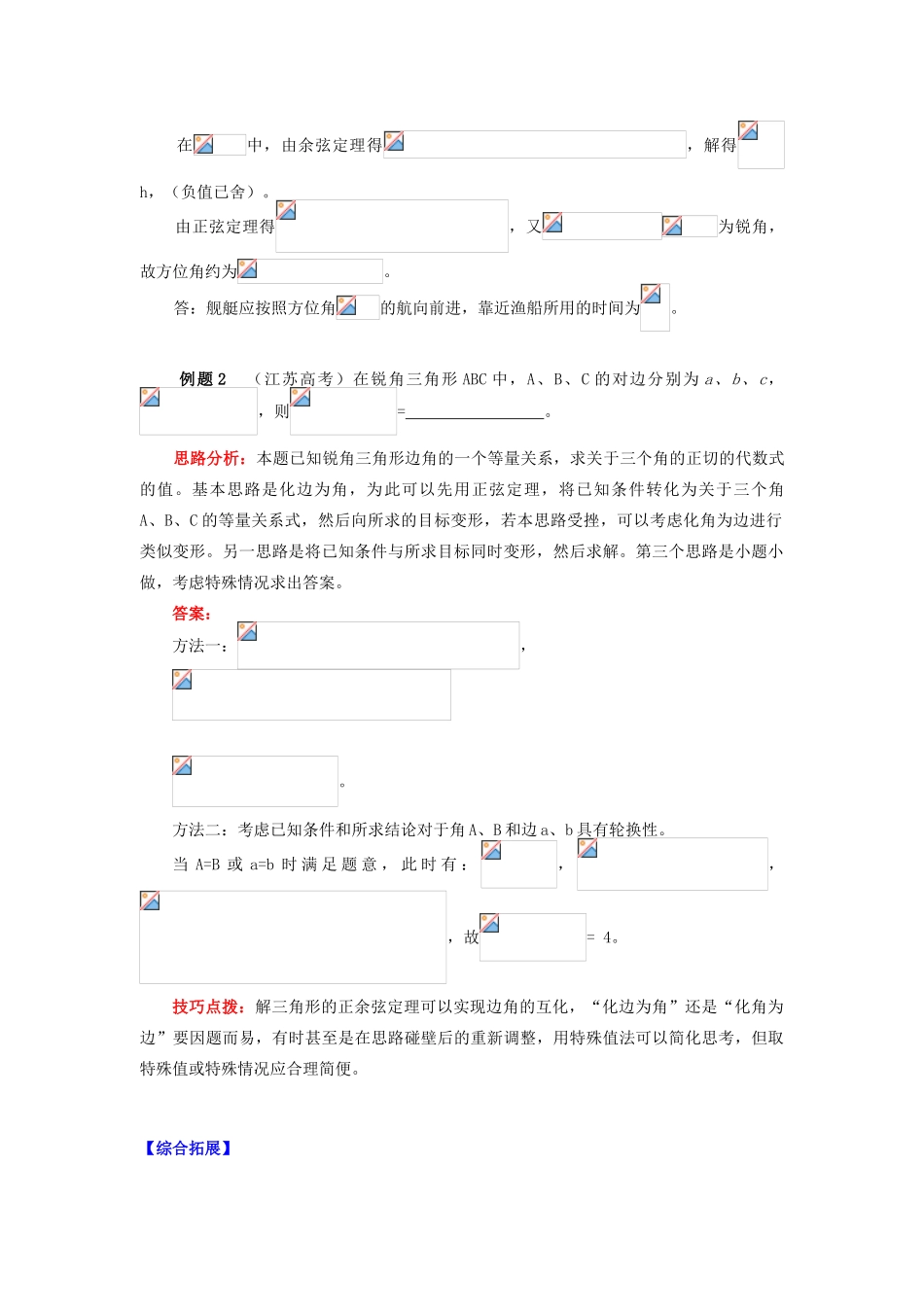
正弦定理、余弦定理的应用一、考点突破知识点课标要求题型说明正弦定理、余弦定理的应用1. 通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。2. 能够运用正弦定理、余弦定理等知识和方法,解决一些与测量和几何计算有关的实际问题。填空题解答题高考必考运用正、余弦定理可以实现边角的互化,不同的转化方向考查了思维的灵活性;解三角形问题经常与三角恒等变换结合,体现了考查的综合性;实际问题需要数学化,体现了数学的应用价值。二、重难点提示重点:正弦定理及余弦定理的灵活运用。难点:运用三角函数及正、余弦定理解决生活中的实际问题。1. 正弦定理及三角形面积公式:,。2. 余弦定理:3. 三角形的边角互化:① ,,②,,③ ==④⑤ 4. 三角形中的基本关系式:5. 利用正弦定理和三角形内角和定理,可以解决以下两类解斜三角形问题:① 已知两角和任一边,求其他两边和一角;② 已知两边和其中一边的对角,求另一边的对角,从而进一步求其他的边和角。(这种类型也可以用余弦定理求解)6. 应用余弦定理解以下两类三角形问题:① 已知三边求三内角;② 已知两边和它们的夹角,求第三边和其他两个内角。7. 实际问题的思考策略审题建模(三角形模型)解模(解三角形求符合题意的边或角)答模(检验并写出实际问题的答案)例题 1 某渔船在航行中不幸遇险,发出求救信号,我海军舰艇在 A 处获悉后,立即测出该渔船在方位角为 45°,距离 A 为 10 n mile 的 C 处,并测得渔船正沿方位角为105°的方向,以 9 n mile/h 的速度向某小岛 B 靠拢,我海军舰艇立即以 21 n mile/h的速度前去营救,试问舰艇应按照怎样的航向前进?并求出靠近渔船所用的时间。思路分析:本题中的自变量是时间 x,有了时间就有了距离,求舰艇的航向就是当舰艇与渔船同时到达点 B 时舰艇的方位角,其大小为。在中,可求,其它三边可表示或已知,用余弦定理列出一个方程即可求出 x。求既可以用余弦定理,也可以用正弦定理,通常用正弦定理运算量稍小些。答案:解:设舰艇在 B 处靠近渔船所用的时间为舰艇 x h,则 AB=21x,BC=9x,又 AC=10,, 在中,由余弦定理得,解得h,(负值已舍)。 由正弦定理得,又为锐角,故方位角约为。答:舰艇应按照方位角的航向前进,靠近渔船所用的时间为。 例题 2 (江苏高考)在锐角三角形 ABC 中,A、B、C 的对边分别为 a、b、...