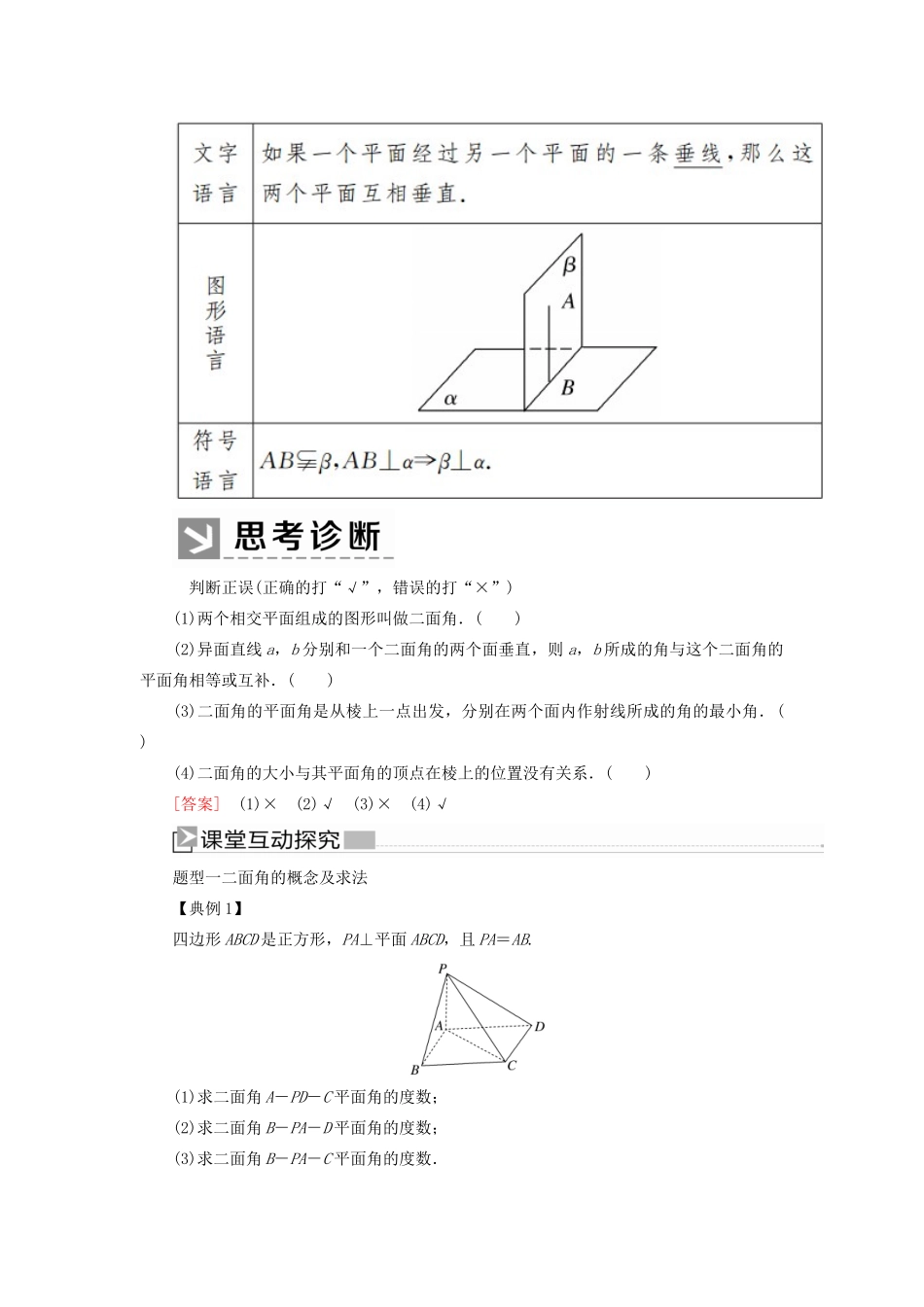
二 平面与平面垂直的判定1.二面角(1)定义:从一条直线出发的两个半平面所组成的图形叫作二面角.这条直线叫作二面角的棱.这两个半平面叫作二面角的面.以直线 AB 为棱、半平面 α,β 为面的二面角,记作二面角α - AB - β (如图①). (2)以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角,如图②中的∠AOB.平面角是直角的二面角叫作直二面角.2.平面与平面的垂直(1)定义:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.(2)画法记作:α ⊥ β .(3)平面和平面垂直的判定定理 判断正误(正确的打“√”,错误的打“×”)(1)两个相交平面组成的图形叫做二面角.( )(2)异面直线 a,b 分别和一个二面角的两个面垂直,则 a,b 所成的角与这个二面角的平面角相等或互补.( )(3)二面角的平面角是从棱上一点出发,分别在两个面内作射线所成的角的最小角.( )(4)二面角的大小与其平面角的顶点在棱上的位置没有关系.( )[答案] (1)× (2)√ (3)× (4)√题型一二面角的概念及求法【典例 1】 四边形 ABCD 是正方形,PA⊥平面 ABCD,且 PA=AB.(1)求二面角 A-PD-C 平面角的度数;(2)求二面角 B-PA-D 平面角的度数;(3)求二面角 B-PA-C 平面角的度数.[思路导引] 根据二面角的平面角的定义,先找出二面角的平面角,然后放在三角形中求角.[解] (1) PA⊥平面 ABCD,∴PA⊥CD.又四边形 ABCD 为正方形,∴CD⊥AD.PA∩AD=A,∴CD⊥平面 PAD.又 CD平面 PCD,∴平面 PAD⊥平面 PCD.∴二面角 A-PD-C 平面角的度数为 90°.(2) PA⊥平面 ABCD,∴AB⊥PA,AD⊥PA.∴∠BAD 为二面角 B-PA-D 的平面角.又由题意知∠BAD=90°,∴二面角 B-PA-D 平面角的度数为 90°.(3) PA⊥平面 ABCD,∴AB⊥PA,AC⊥PA.∴∠BAC 为二面角 B-PA-C 的平面角.又四边形 ABCD 为正方形,∴∠BAC=45°,即二面角 B-PA-C 平面角的度数为 45°.(1)求二面角大小的步骤简称为“一作二证三求”.(2)求二面角的方法①(定义法):在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.如图(1)所示,∠AOB 为二面角 α-a-β 的平面角.②(垂线法):过二面角的一个面内一点作另一个平面的垂线,过垂足作棱的垂线,连接该点与垂足,利用线面垂直可找到二面角的平面角或其补角.如图(2)所示,∠AFE 为...