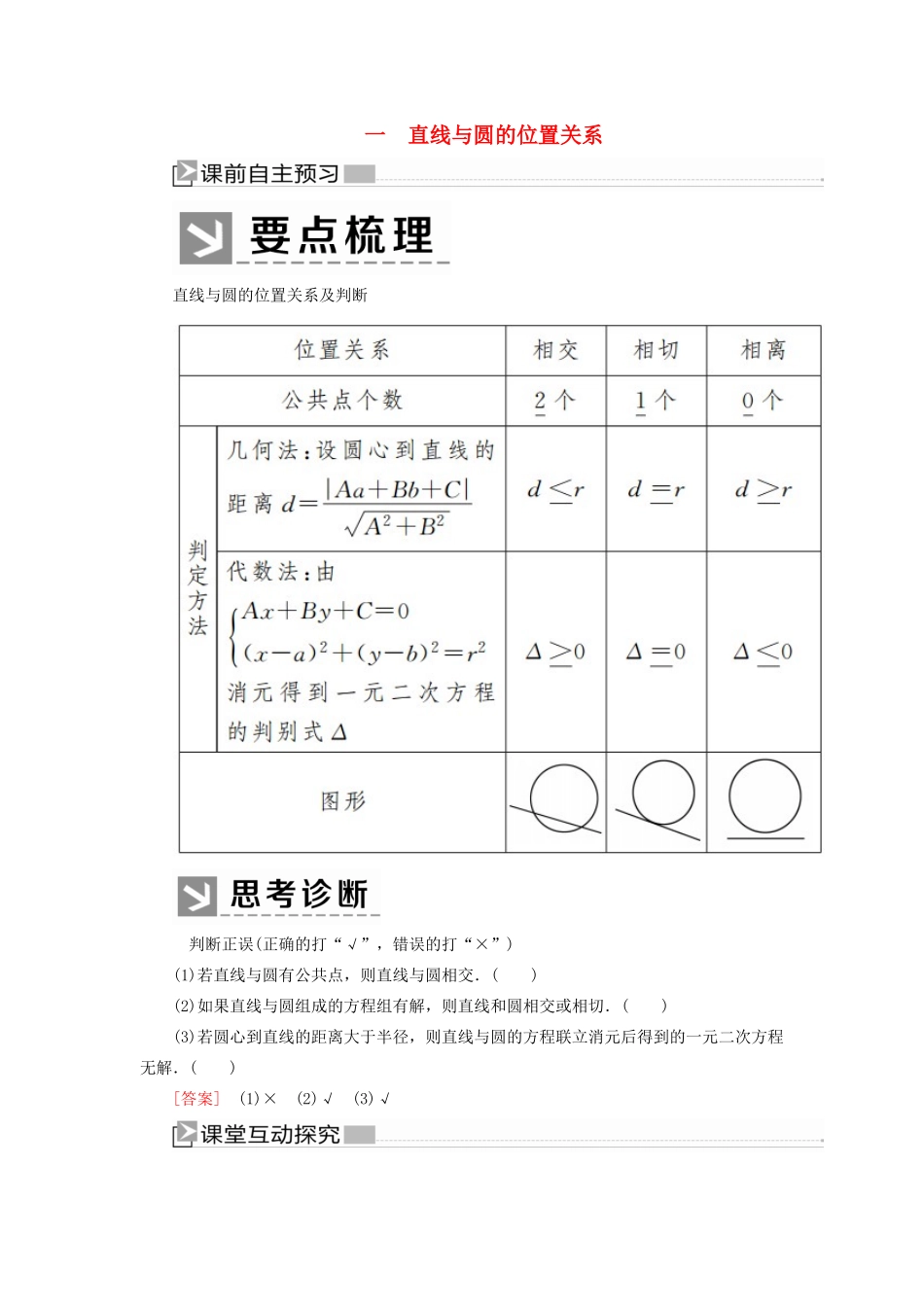
一 直线与圆的位置关系直线与圆的位置关系及判断 判断正误(正确的打“√”,错误的打“×”)(1)若直线与圆有公共点,则直线与圆相交.( )(2)如果直线与圆组成的方程组有解,则直线和圆相交或相切.( )(3)若圆心到直线的距离大于半径,则直线与圆的方程联立消元后得到的一元二次方程无解.( )[答案] (1)× (2)√ (3)√题型一直线与圆的位置关系的判定【典例 1】 已知圆 C:x2+y2=1 与直线 y=kx-3k,当 k 为何值时,直线与圆(1)相交;(2)相切;(3)相离. [解] 解法一(代数法):联立消去 y, 整理得(k2+1)x2-6k2x+9k2-1=0. Δ=(-6k2)2-4(k2+1)(9k2-1) =-32k2+4=4(1-8k2). (1)当直线与圆相交时,Δ>0,即-.解法二(几何法):圆心(0,0)到直线 y=kx-3k 的距离 d==.由条件知,圆的半径为 r=1. (1)当直线与圆相交时,dr, 即>1,得 k<-或 k>. 直线与圆位置关系判断的三种方法(1)几何法:由圆心到直线的距离 d 与圆的半径 r 的大小关系判断;(2)代数法:根据直线与圆的方程组成的方程组解的个数来判断;(3)直线系法:若直线恒过定点,可通过判断点与圆的位置关系判断,但有一定的局限性,必须是过定点的直线系.[针对训练 1] (1)直线 x-ky+1=0 与圆 x2+y2=1 的位置关系是( )A.相交 B.相离C.相交或相切D.相切(2)过点 P(-,-1)的直线 l 与圆 x2+y2=1 有公共点,则直线 l 的倾斜角 α 的取值范围是________.[解析] (1)由直线 x-ky+1=0 恒过定点(-1,0), 而(-1,0)恰在圆 x2+y2=1 上,故直线与圆至少有一个公共点,故选 C. (2)当直线 l 斜率不存在时,直线 l 与圆 x2+y2=1 没有公共点,故可设直线 y+1=k(x+),即 kx-y+k-1=0,圆心到直线的距离≤1,解得 0≤k≤,即 0≤tanα≤,即 0≤α≤.[答案] (1)C (2)题型二圆的切线问题【典例 2】 过点 A(4,-3)作圆(x-3)2+(y-1)2=1 的切线,求此切线的方程.[思路导引] 设直线的点斜式方程,利用圆心到直线的距离等于半径求出斜率,注意斜率不存在的情况.[解] 因为(4-3)2+(-3-1)2=17>1,所以点 A 在圆外.(1)若所求直线的斜率存在,设切线斜率为 k,则切线方程为 y+3=k(x-4)...