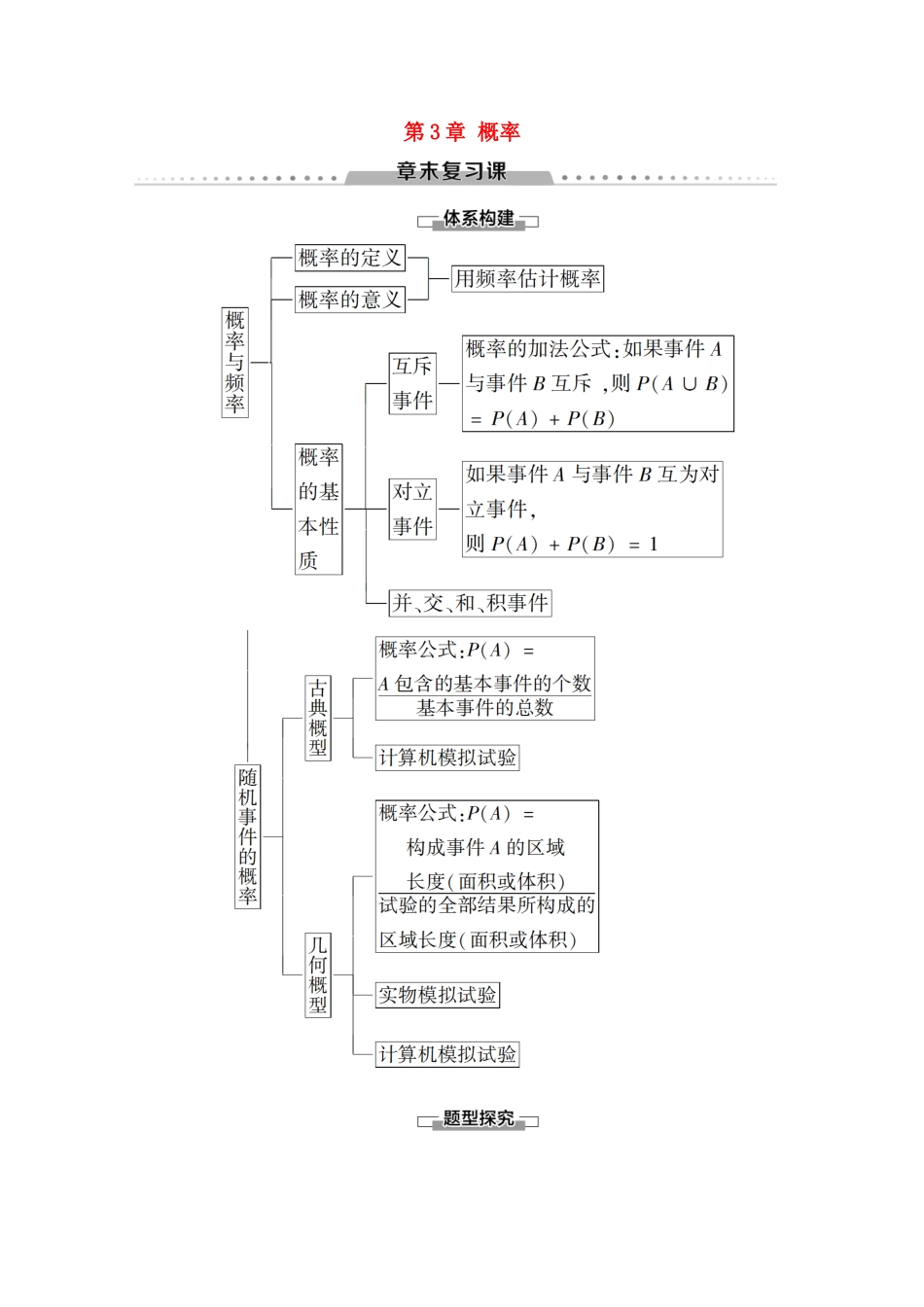
第 3 章 概率用频率估计概率【例 1】 为了为奥运会做准备,某射击运动员在相同条件下进行射击训练,结果如下表:射击次数 n102050100200500击中靶心次数 m8194492178455击中靶心的频率0.80.950.880.920.890.91(1)该射击运动员射击一次,击中靶心的概率大约是多少?(2)假设该射击运动员射击了 300 次,则击中靶心的次数大约是多少?(3)假设该射击运动员射击了 10 次,前 9 次中有 8 次击中靶心,那么第 10 次一定击中靶心吗?[解] (1)由表可知,击中靶心的频率在 0.9 附近,故击中靶心的概率大约是 0.9.(2)击中靶心的次数大约是 300×0.9=270(次).(3)由概率的意义,可知概率是个常数,不因试验次数的变化而变化.最后一次击中靶心的概率仍是 0.9,所以不一定击中靶心.概率是一个常数,但除了特殊几类概型,概率并不易知,故可以用频率来估计.1.对一批 U 盘进行抽检,结果如下表:抽出件数 a50100200300400500次品件数 b345589次品频率(1)计算表中次品的频率;(2)从这批 U 盘中任意抽取一个是次品的概率约是多少?(3)为保证买到次品的顾客能够及时更换,要销售 2 000 个 U 盘,至少需进货多少个 U 盘?[解] (1)表中次品频率从左到右依次为 0.06,0.04,0.025,0.017,0.02,0.018.(2)当抽取件数 a 越来越大时,出现次品的频率在 0.02 附近摆动,所以从这批 U 盘中任意抽取一个是次品的概率约是 0.02.(3)设需要进货 x 个 U 盘,为保证其中有 2 000 个正品 U 盘,则 x(1-0.02)≥2 000,因为 x 是正整数,所以 x≥2 041,即至少需进货 2 041 个 U 盘.互斥事件与对立事件的概率【例 2】 某商场有奖销售中,购满 100 元商品得一张奖券,多购多得,每 1 000 张奖券为一个开奖单位.设特等奖 1 个,一等奖 10 个,二等奖 50 个.设 1 张奖券中特等奖、一等奖、二等奖的事件分别为 A,B,C,求:(1)P(A),P(B),P(C);(2)抽取 1 张奖券中奖的概率;(3)抽取 1 张奖券不中特等奖或一等奖的概率.[解] 由题意事件 A、B、C 为互斥事件.(1) 每 1 000 张奖券中设特等奖 1 个,一等奖 10 个,二等奖 50 个,∴P(A)=,P(B)==,P(C)==.(2)设“抽取 1 张奖券中奖”为事件 D,则P(D)=P(A)+P(B)+P(C)=++=.(3)设“抽取 1 张奖券不中特等奖或一等奖”为事件 E,则P(E)=1-P(A)-P(B)=1--=.]求复杂事件的概率通常有两种方法一是将所求事...