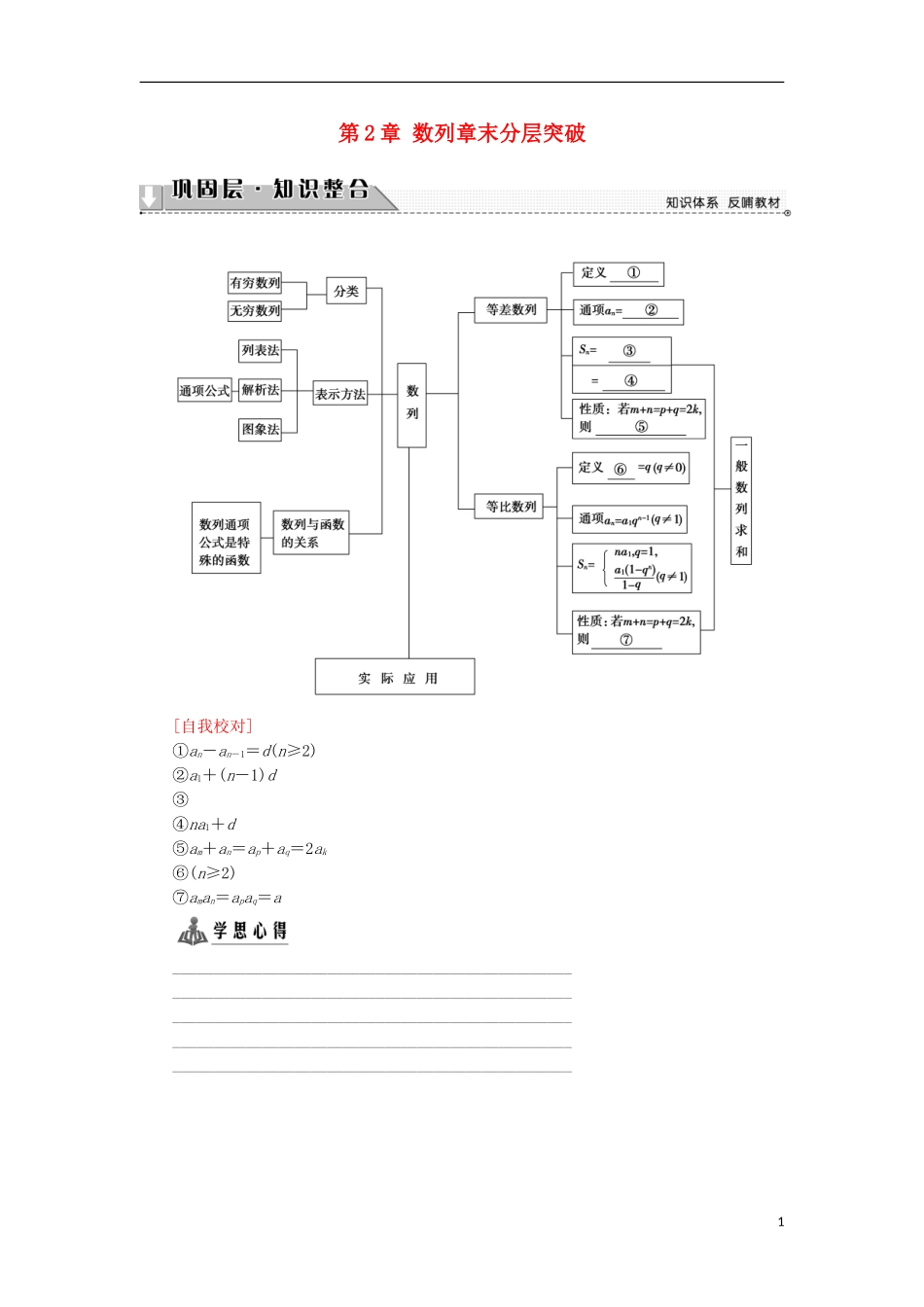
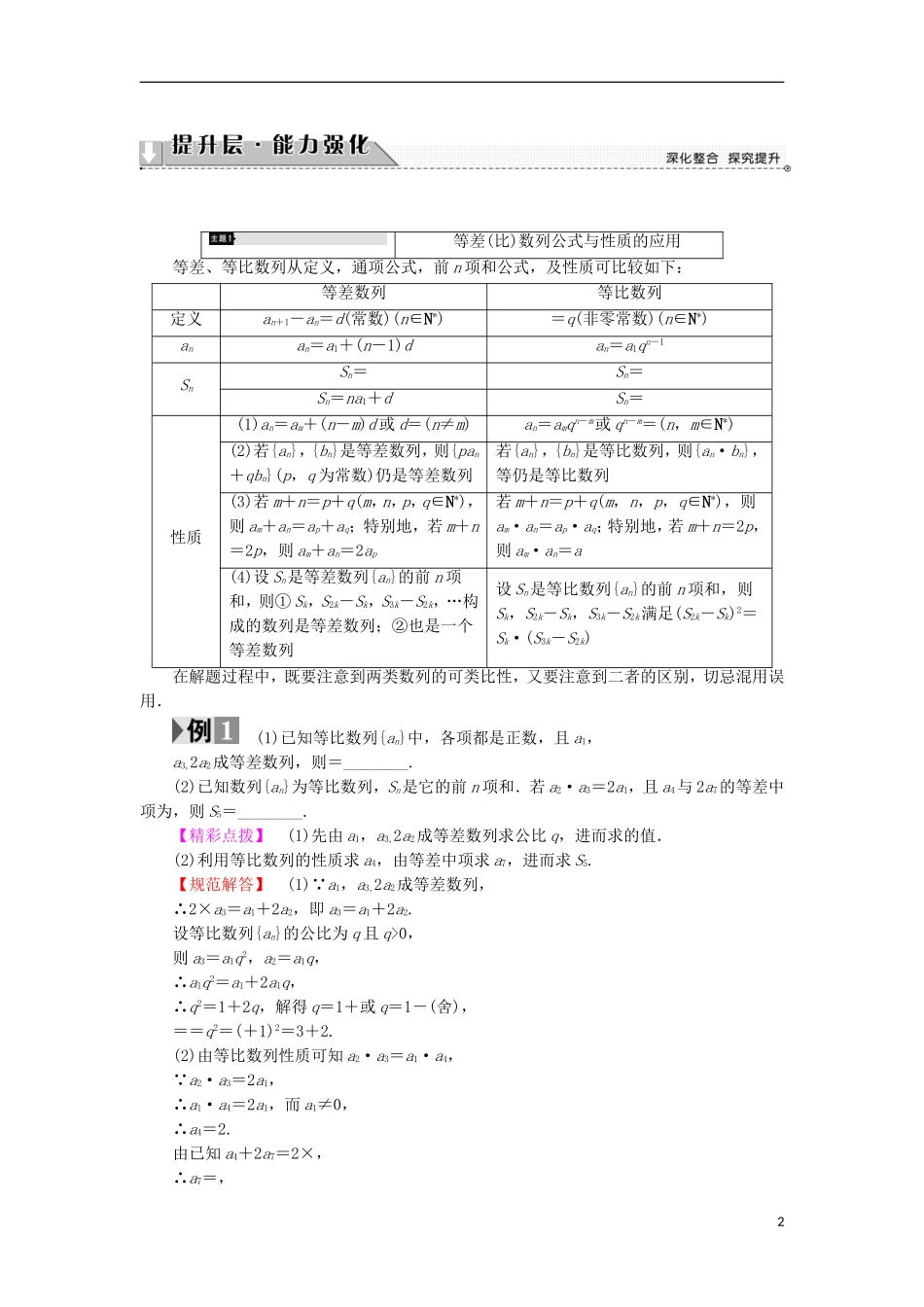
第 2 章 数列章末分层突破[自我校对]①an-an-1=d(n≥2)②a1+(n-1)d③④na1+d⑤am+an=ap+aq=2ak⑥(n≥2)⑦aman=apaq=a_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________1 等差(比)数列公式与性质的应用等差、等比数列从定义,通项公式,前 n 项和公式,及性质可比较如下:等差数列等比数列定义an+1-an=d(常数)(n∈N*)=q(非零常数)(n∈N*)anan=a1+(n-1)dan=a1qn-1SnSn=Sn=Sn=na1+dSn=性质(1)an=am+(n-m)d 或 d=(n≠m)an=amqn-m或 qn-m=(n,m∈N*)(2)若{an},{bn}是等差数列,则{pan+qbn}(p,q 为常数)仍是等差数列若{an},{bn}是等比数列,则{an·bn},等仍是等比数列(3)若 m+n=p+q(m,n,p,q∈N*),则 am+an=ap+aq;特别地,若 m+n=2p,则 am+an=2ap若 m+n=p+q(m,n,p,q∈N*),则am·an=ap·aq;特别地,若 m+n=2p,则 am·an=a(4)设 Sn是等差数列{an}的前 n 项和,则① Sk,S2k-Sk,S3k-S2k,…构成的数列是等差数列;②也是一个等差数列设 Sn是等比数列{an}的前 n 项和,则Sk,S2k-Sk,S3k-S2k满足(S2k-Sk)2=Sk·(S3k-S2k)在解题过程中,既要注意到两类数列的可类比性,又要注意到二者的区别,切忌混用误用. (1)已知等比数列{an}中,各项都是正数,且 a1,a3,2a2成等差数列,则=________.(2)已知数列{an}为等比数列,Sn是它的前 n 项和.若 a2·a3=2a1,且 a4与 2a7的等差中项为,则 S5=________.【精彩点拨】 (1)先由 a1,a3,2a2成等差数列求公比 q,进而求的值.(2)利用等比数列的性质求 a4,由等差中项求 a7,进而求 S5.【规范解答】 (1) a1,a3,2a2成等差数列,∴2×a3=a1+2a2,即 a3=a1+2a2.设等比数列{an}的公比为 q 且 q>0,则 a3=a1q2,a2=a1q,∴a1q2=a1+2a1q,∴q2=1+2q,解得 q=1+或 q=1-(舍),==q2=(+1)2=3+2.(2)由等比数列性质可知 a2·a3=a1·a4, a2·a3=2a1,∴a1·a4=2a1,而 a1≠0,∴a4=2.由已知 a4+2a7=2×,∴a7=,2∴q3==,∴q=,∴a1===16,∴S5===31.【答案】 (1)3+2 (2)31[再练一题]1.成等差数列的三个正数的和等于 15,并且这三个数分别...