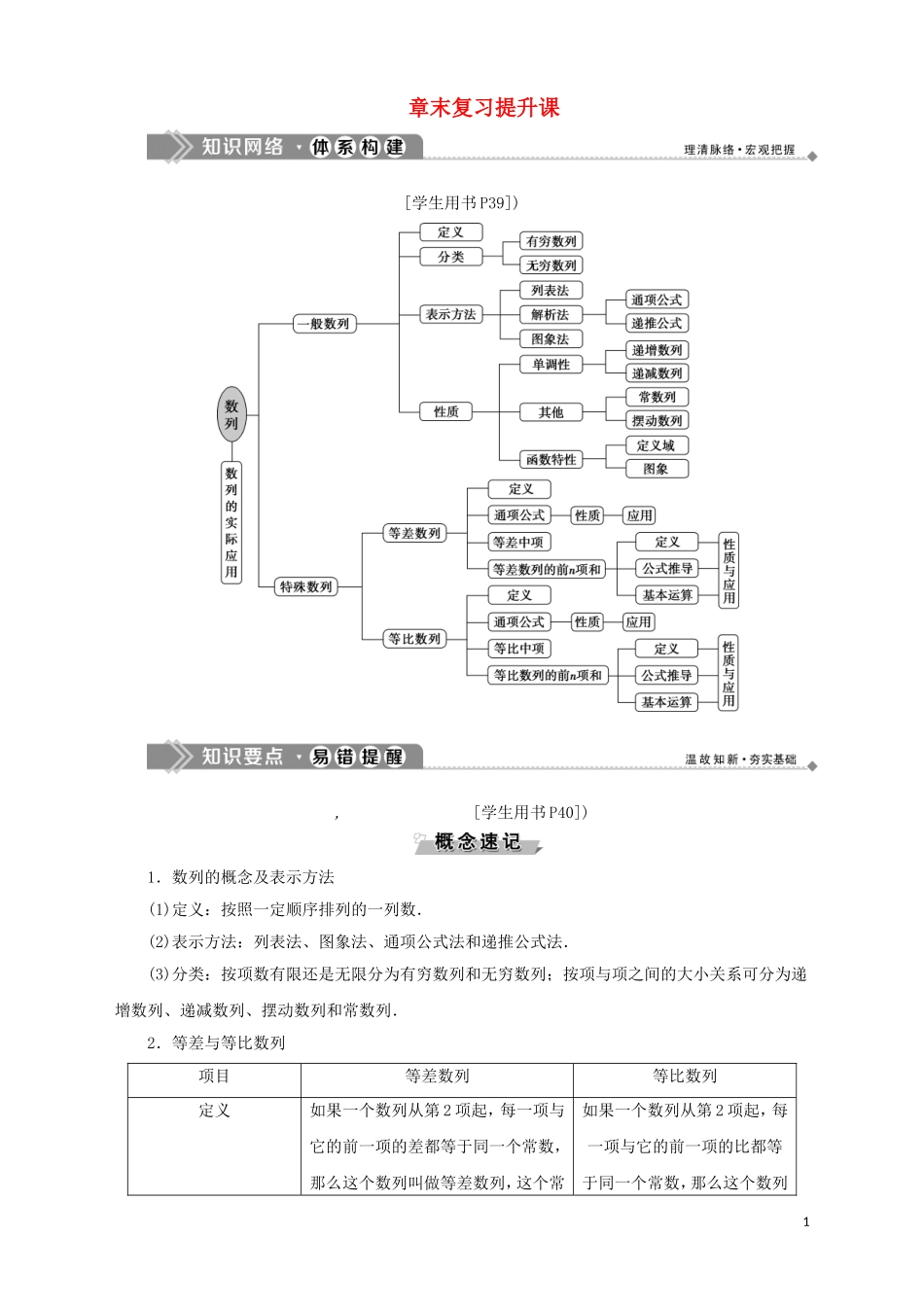
章末复习提升课 [学生用书 P39]), [学生用书 P40])1.数列的概念及表示方法(1)定义:按照一定顺序排列的一列数.(2)表示方法:列表法、图象法、通项公式法和递推公式法.(3)分类:按项数有限还是无限分为有穷数列和无穷数列;按项与项之间的大小关系可分为递增数列、递减数列、摆动数列和常数列.2.等差与等比数列项目等差数列等比数列定义如果一个数列从第 2 项起,每一项与它的前一项的差都等于同一个常数,那么这个数列叫做等差数列,这个常如果一个数列从第 2 项起,每一项与它的前一项的比都等于同一个常数,那么这个数列1数叫做公差,通常用字母 d 表示叫做等比数列,这个常数叫做公比,通常用字母 q 表示递推关系an+1-an=d=q通项公式an=a1+(n-1)dan=a1qn-1an=am+(n-m)dan=amqn-m中项若三个数 a,A,b 成等差数列,这时 A叫做 a 与 b 的等差中项,且 A=若三个数 a,G,b 成等比数列,这时 G 叫做 a 与 b 的等比中项,且 G=±前 n 项和公式Sn==na1+dSn==(q≠1)Sn=na1(q=1)判断方法定义法an+1-an是同一个常数是同一个常数中项法an+an+2=2an+1anan+2=a通项公式法an=pn+qan=pqnSn的形式当 d≠0 时,Sn是不含常数项的二次函数当 q≠1 时,Sn中只有 qn与常数项,且系数互为相反数性质下标性质m、n、p、q∈N*且 m+n=p+qam+an=ap+aqam·an=ap·aqSm,S2m-Sm,S3m-S2m…成等差数列当公比 q≠-1 时成等比数列1.辨明等差(比)数列的定义等差(比)数列的定义中都强调从第 2 项开始,每一项与前一项的差(比),是同一常数.利用定义法证明等差(比)数列时,要特别注意 n 的取值范围.2.“数清”数列的项数在解答数列问题时,及时准确地“数清”数列的项数是必不可少的,在数项数时,要把握数列的项的构成规律,找准数列的通项公式的特点并找准项数.如果把数列的项数弄错了,将会前功尽弃.3.注意分类讨论(1)应用 an=解题时,应注意分类讨论的应用,即要注意分 n=1 和 n≥2 两种情况进行讨论.(2)等比数列中,奇数项(或偶数项)的符号相同,解题时常因忽略这点而致误., [学生用书 P41])2 等差、等比数列的判定 设数列{an}的前 n 项和为 Sn,n∈N*.已知 a1=1,a2=,a3=,且当 n≥2 时,4Sn+2+5Sn=8Sn+1+Sn-1.(1)求 a4的值;(2)证明:为等比数列.[解] (1)当 n=2 时,4S4+5S2=8S3+S1,即 4+5=8+1,解得 a4=.(2)证明:由 ...