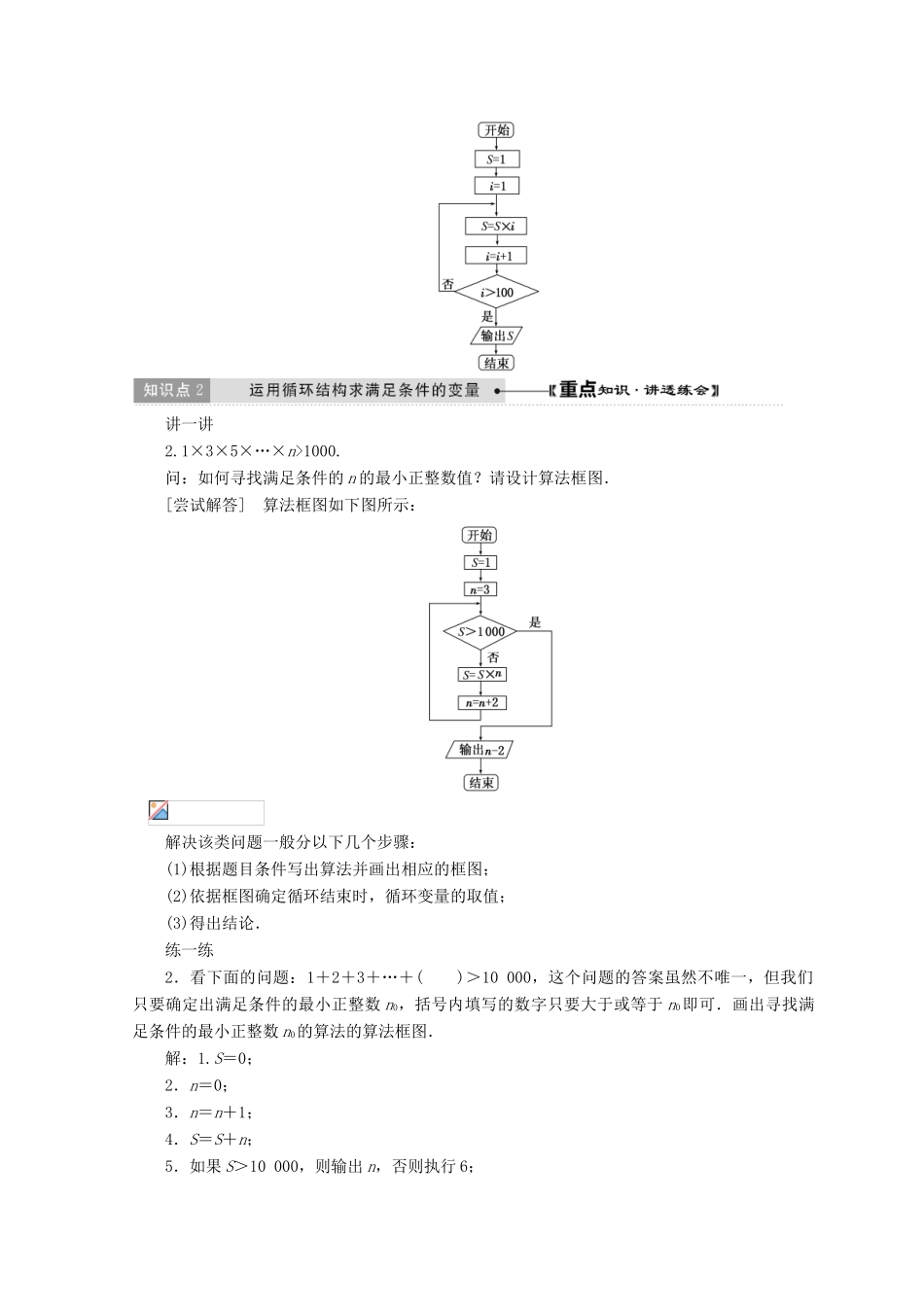
第 3 课时 循环结构[核心必知]1.循环结构的概念在算法中,从某处开始,按照一定的条件反复执行某些步骤的结构称为循环结构,用算法框图如图所示.反复执行的部分称为循环体,控制着循环的开始和结束的变量,称为循环变量,决定是否继续执行循环体的判断条件,称为循环的终止条件.2.循环结构的设计过程设计循环结构之前需要确定的三件事:(1)确定循环变量和初始值;(2)确定算法中反复执行的部分,即循环体;(3)确定循环的终止条件.循环结构的算法框图的基本模式,如图所示.[问题思考]1.循环结构中一定含有选择结构吗?提示:在循环结构中需要判断是否继续循环,故循环结构中一定含有选择结构.2.循环结构中判断框中条件是唯一的吗?提示:不是,在具体的算法框图设计时,判断框中的条件可以不同,但不同的表示应该有共同的确定的结果.3.算法框图的基本结构有哪些?提示:顺序结构、选择结构和循环结构. 讲一讲1.利用循环结构写出++…+的算法并画出相应的算法框图.[尝试解答] 算法如下:1.S=0;2.i=1;3.S=S+;4.i=i+1;5.如果 i 不大于 100,转第 3 步,否则输出 S.相应框图如下图表示:1.如果算法问题中涉及到的运算进行了多次重复,且参与运算的数前后有规律可循,就可以引入变量以参与循环结构.2.在不同的循环结构中,应注意判断条件的差别,及计数变量和累加(乘)变量的初始值与运算框先后关系的对应性.练一练1.利用循环结构写出 1×2×3×…×100 的算法.并画出相应的框图.解:算法步骤如下:1.S=1;2.i=1;3.S=S×i;4.i=i+1;5.判断 i 是否大于 100,若成立,则输出 S,结束算法;否则返回第 3 步重新执行.算法框图如图所示:讲一讲2.1×3×5×…×n>1000.问:如何寻找满足条件的 n 的最小正整数值?请设计算法框图.[尝试解答] 算法框图如下图所示:解决该类问题一般分以下几个步骤:(1)根据题目条件写出算法并画出相应的框图;(2)依据框图确定循环结束时,循环变量的取值;(3)得出结论. 练一练2.看下面的问题:1+2+3+…+( )>10 000,这个问题的答案虽然不唯一,但我们只要确定出满足条件的最小正整数 n0,括号内填写的数字只要大于或等于 n0即可.画出寻找满足条件的最小正整数 n0的算法的算法框图.解:1.S=0;2.n=0;3.n=n+1;4.S=S+n;5.如果 S>10 000,则输出 n,否则执行 6;6.回到 3,重新执行 4,5.框图如右图:讲一讲3.某高中男子...