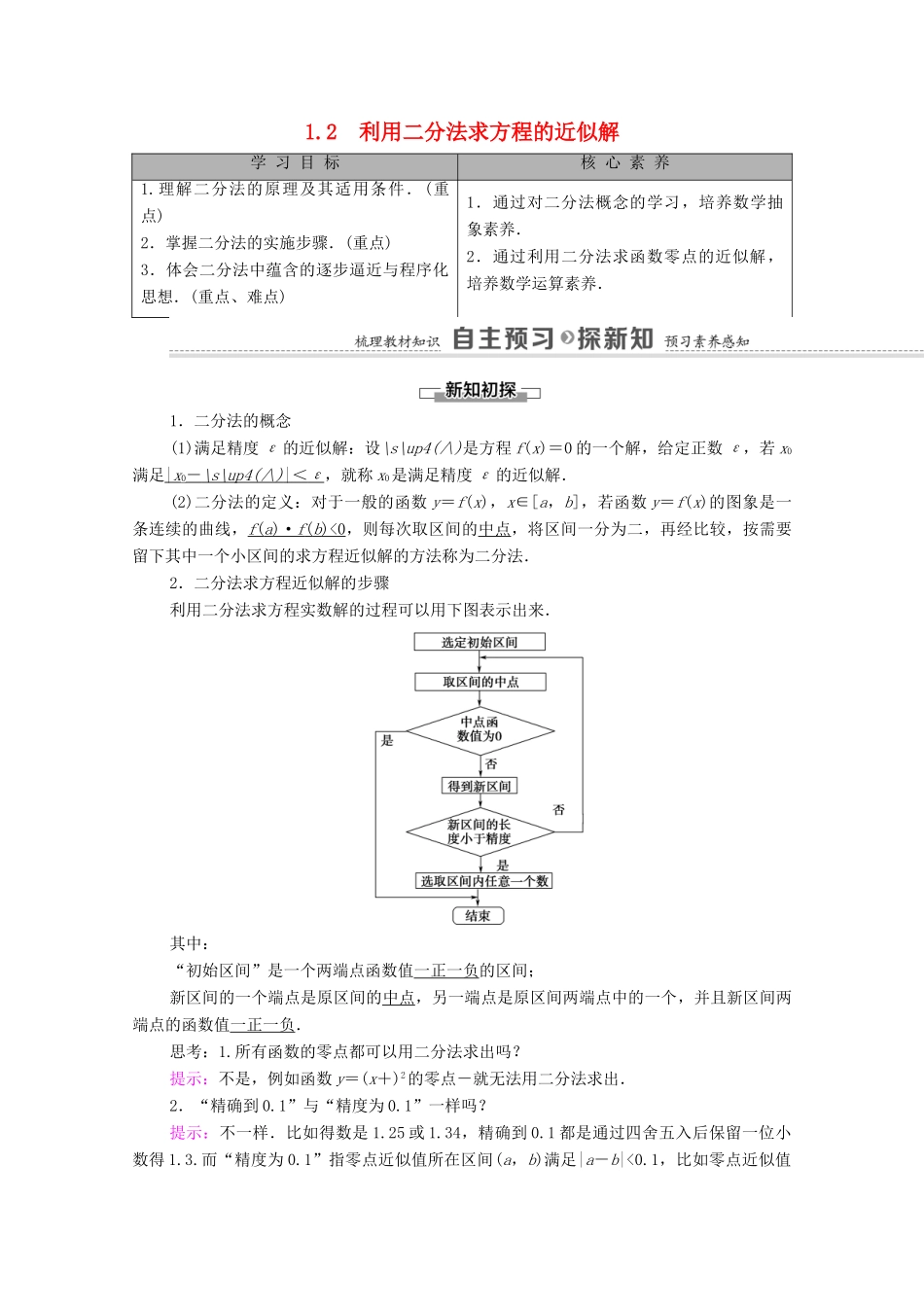
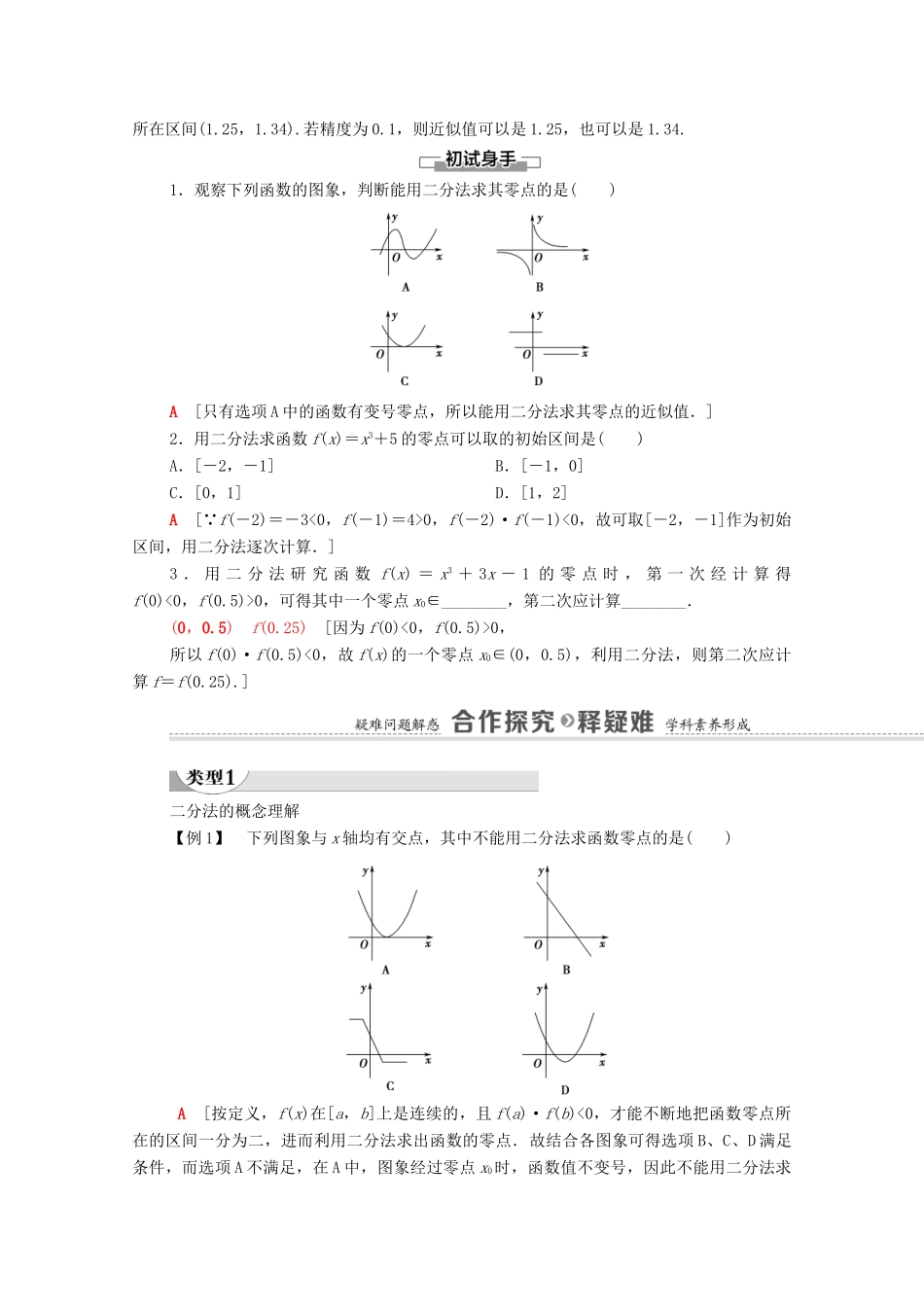
1.2 利用二分法求方程的近似解学 习 目 标核 心 素 养1.理解二分法的原理及其适用条件.(重点)2.掌握二分法的实施步骤.(重点)3.体会二分法中蕴含的逐步逼近与程序化思想.(重点、难点)1.通过对二分法概念的学习,培养数学抽象素养.2.通过利用二分法求函数零点的近似解,培养数学运算素养.1.二分法的概念(1)满足精度 ε 的近似解:设\s\up4(∧)是方程 f(x)=0 的一个解,给定正数 ε,若 x0满足| x 0- \s\up4(∧) | < ε ,就称 x0是满足精度 ε 的近似解.(2)二分法的定义:对于一般的函数 y=f(x),x∈[a,b],若函数 y=f(x)的图象是一条连续的曲线,f ( a )· f ( b )<0 ,则每次取区间的中点,将区间一分为二,再经比较,按需要留下其中一个小区间的求方程近似解的方法称为二分法.2.二分法求方程近似解的步骤利用二分法求方程实数解的过程可以用下图表示出来.其中:“初始区间”是一个两端点函数值一正一负的区间;新区间的一个端点是原区间的中 点 ,另一端点是原区间两端点中的一个,并且新区间两端点的函数值一正一负.思考:1.所有函数的零点都可以用二分法求出吗?提示:不是,例如函数 y=(x+)2的零点-就无法用二分法求出.2.“精确到 0.1”与“精度为 0.1”一样吗?提示:不一样.比如得数是 1.25 或 1.34,精确到 0.1 都是通过四舍五入后保留一位小数得 1.3.而“精度为 0.1”指零点近似值所在区间(a,b)满足|a-b|<0.1,比如零点近似值所在区间(1.25,1.34).若精度为 0.1,则近似值可以是 1.25,也可以是 1.34.1.观察下列函数的图象,判断能用二分法求其零点的是( )A [只有选项 A 中的函数有变号零点,所以能用二分法求其零点的近似值.]2.用二分法求函数 f(x)=x3+5 的零点可以取的初始区间是( )A.[-2,-1] B.[-1,0]C.[0,1] D.[1,2]A [ f(-2)=-3<0,f(-1)=4>0,f(-2)·f(-1)<0,故可取[-2,-1]作为初始区间,用二分法逐次计算.]3 . 用 二 分 法 研 究 函 数 f(x) = x3 + 3x - 1 的 零 点 时 , 第 一 次 经 计 算 得f(0)<0,f(0.5)>0,可得其中一个零点 x0∈________,第二次应计算________.(0,0.5) f(0.25) [因为 f(0)<0,f(0.5)>0,所以 f(0)·f(0.5)<0,故 f(x)的一个零点 x0∈(0,0.5),利用二分法,则第二次应计算 f=f(0.25).]二分法的概念理解【例 1】 下列图象与 x 轴均...