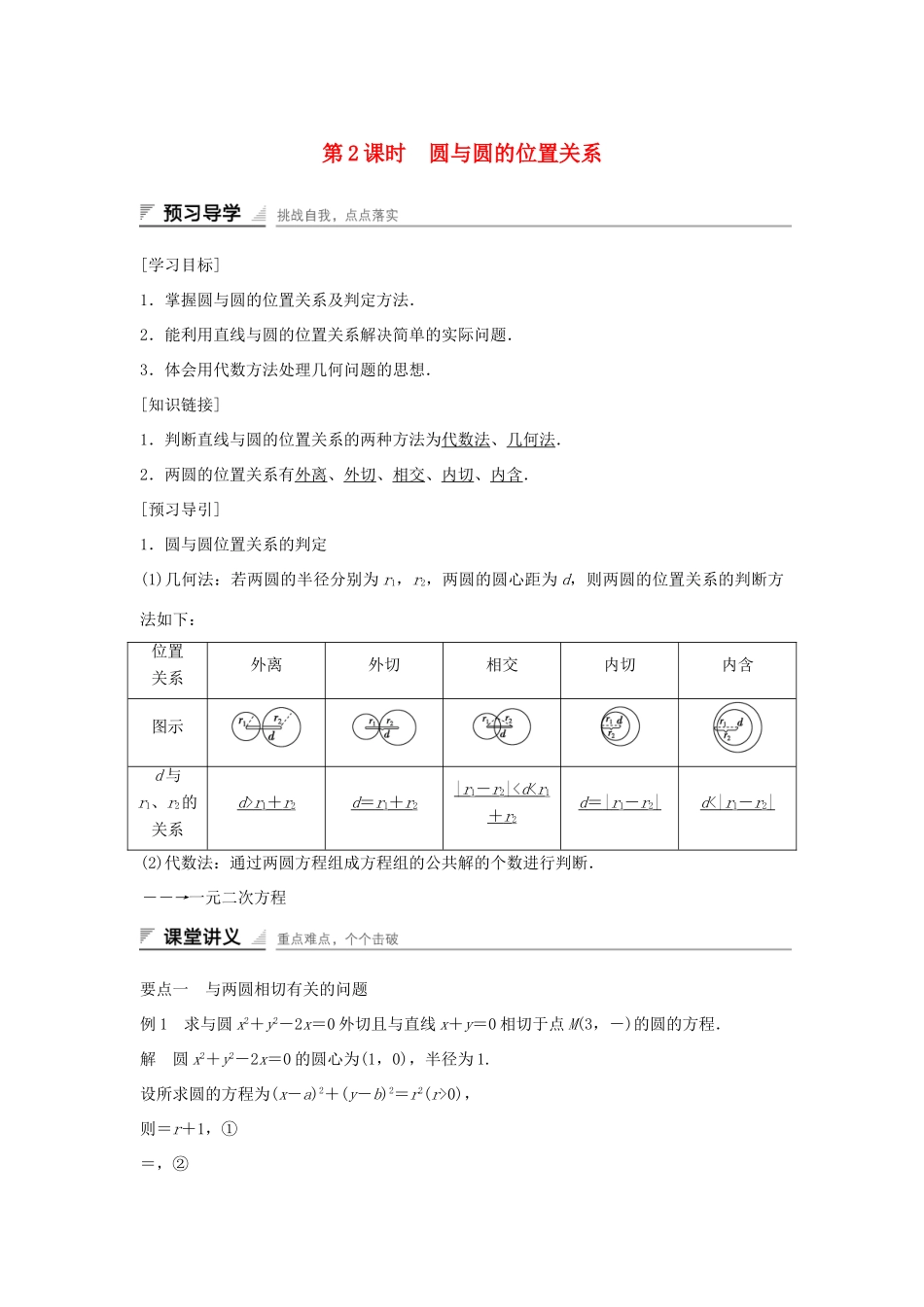
第 2 课时 圆与圆的位置关系[学习目标]1.掌握圆与圆的位置关系及判定方法.2.能利用直线与圆的位置关系解决简单的实际问题.3.体会用代数方法处理几何问题的思想.[知识链接]1.判断直线与圆的位置关系的两种方法为代数法、几何法.2.两圆的位置关系有外离、外切、相交、内切、内含.[预习导引]1.圆与圆位置关系的判定(1)几何法:若两圆的半径分别为 r1,r2,两圆的圆心距为 d,则两圆的位置关系的判断方法如下:位置关系外离外切相交内切内含图示d 与r1、r2的关系d > r 1+ r 2d = r 1+ r 2| r 1- r 2|< d < r 1+ r 2d = | r 1- r 2|d <| r 1- r 2|(2)代数法:通过两圆方程组成方程组的公共解的个数进行判断.――→一元二次方程要点一 与两圆相切有关的问题例 1 求与圆 x2+y2-2x=0 外切且与直线 x+y=0 相切于点 M(3,-)的圆的方程.解 圆 x2+y2-2x=0 的圆心为(1,0),半径为 1.设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),则=r+1,①=,②=r.③解①②③解得 a=4,b=0,r=2,或 a=0,b=-4,r=6,故所求圆的方程为(x-4)2+y2=4 或 x2+(y+4)2=36.规律方法 两圆相切时常用的性质有:(1)设两圆的圆心分别为 O1,O2,半径分别为 r1,r2,则两圆相切(2)两圆相切时,两圆圆心的连线过切点(两圆若相交时,两圆圆心的连线垂直平分公共弦).跟踪演练 1 求与圆(x-2)2+(y+1)2=4 相切于点 A(4,-1)且半径为 1 的圆的方程.解 设所求圆的圆心为 P(a,b),则=1.①(1)若两圆外切,则有=1+2=3,②联立①②,解得 a=5,b=-1,所以,所求圆的方程为(x-5)2+(y+1)2=1;(2)若两圆内切,则有=|2-1|=1,③联立①③,解得 a=3,b=-1,所以,所求圆的方程为(x-3)2+(y+1)2=1.综上所述,所求圆的方程为(x-5)2+(y+1)2=1 或(x-3)2+(y+1)2=1.要点二 与两圆相交有关的问题例 2 已知圆 C1:x2+y2+2x-6y+1=0,圆 C2:x2+y2-4x+2y-11=0,求两圆的公共弦所在的直线方程及公共弦长.解 设两圆交点为 A(x1,y1),B(x2,y2),则 A,B 两点坐标是方程组的解,①-②得:3x-4y+6=0. A,B 两点坐标都满足此方程,∴3x-4y+6=0 即为两圆公共弦所在的直线方程.易知圆 C1的圆心(-1,3),半径 r1=3.又 C1到直线 AB 的距离为 d==.∴|AB|=2=2=,即两圆的公共弦长为.规律方法 1.两圆相交时,公共弦所在的...