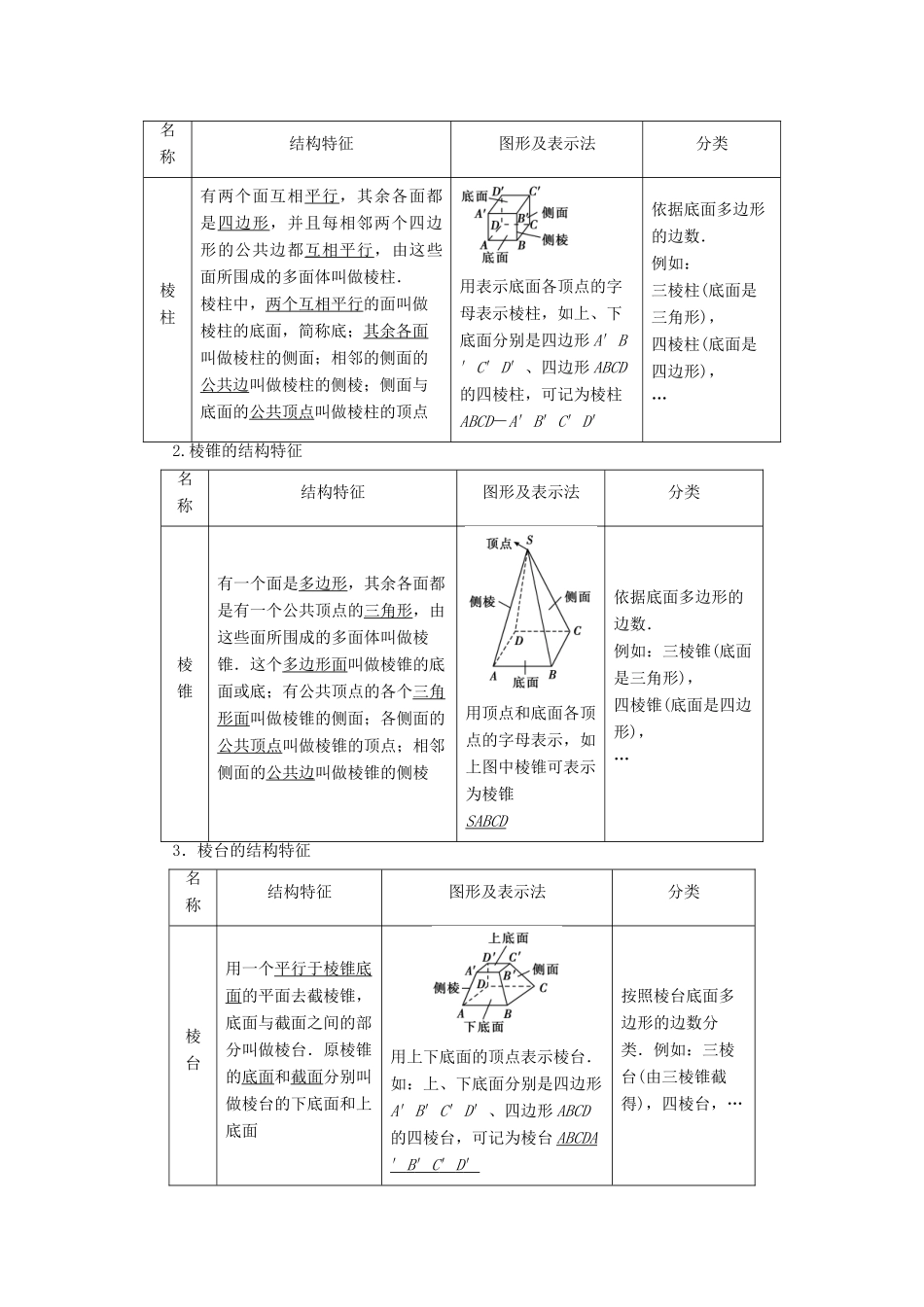
1.1.1 棱柱、棱锥、棱台的结构特征1.通过对实物模型的观察,归纳认知棱柱、棱锥、棱台的结构特征.(重点)2.理解棱柱、棱锥、棱台之间的关系.(难点)3.能运用棱柱、棱锥、棱台的结构特征描述现实生活中简单物体的结构和有关计算.(易混点)[基础·初探]教材整理 1 空间几何体的定义、分类及相关概念阅读教材 P2~P3的内容,完成下列问题.1.空间几何体的定义及分类(1)定义:如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.(2)分类:常见的空间几何体有多面体与旋转体两类.2.多面体与旋转体类别多面体旋转体定义由若干个平面多边形围成的几何体由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体图形相关概念面:围成多面体的各个多边形;棱:相邻两个面的公共边;顶点:棱与棱的公共点轴:形成旋转体所绕的定直线下列物体不能抽象成旋转体的是________.① 篮球;②日光灯管;③电线杆;④金字塔.【答案】 ④教材整理 2 棱柱、棱锥、棱台的结构特征阅读教材 P3~P4的内容,完成下列问题.1.棱柱的结构特征名称结构特征图形及表示法分类棱柱有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;相邻的侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点用表示底面各顶点的字母表示棱柱,如上、下底面分别是四边形 A′B′C′D′、四边形 ABCD的四棱柱,可记为棱柱ABCD-A′B′C′D′依据底面多边形的边数.例如:三棱柱(底面是三角形),四棱柱(底面是四边形),…2.棱锥的结构特征名称结构特征图形及表示法分类棱锥有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱用顶点和底面各顶点的字母表示,如上图中棱锥可表示为棱锥S ABCD 依据底面多边形的边数.例如:三棱锥(底面是三角形),四棱锥(底面是四边形),…3.棱台的结构特征名称结构特征图形及表示法分类棱台用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台.原棱锥的底面和截面分别叫做棱台的下底面和上底面用上下底面的顶点表示棱台...