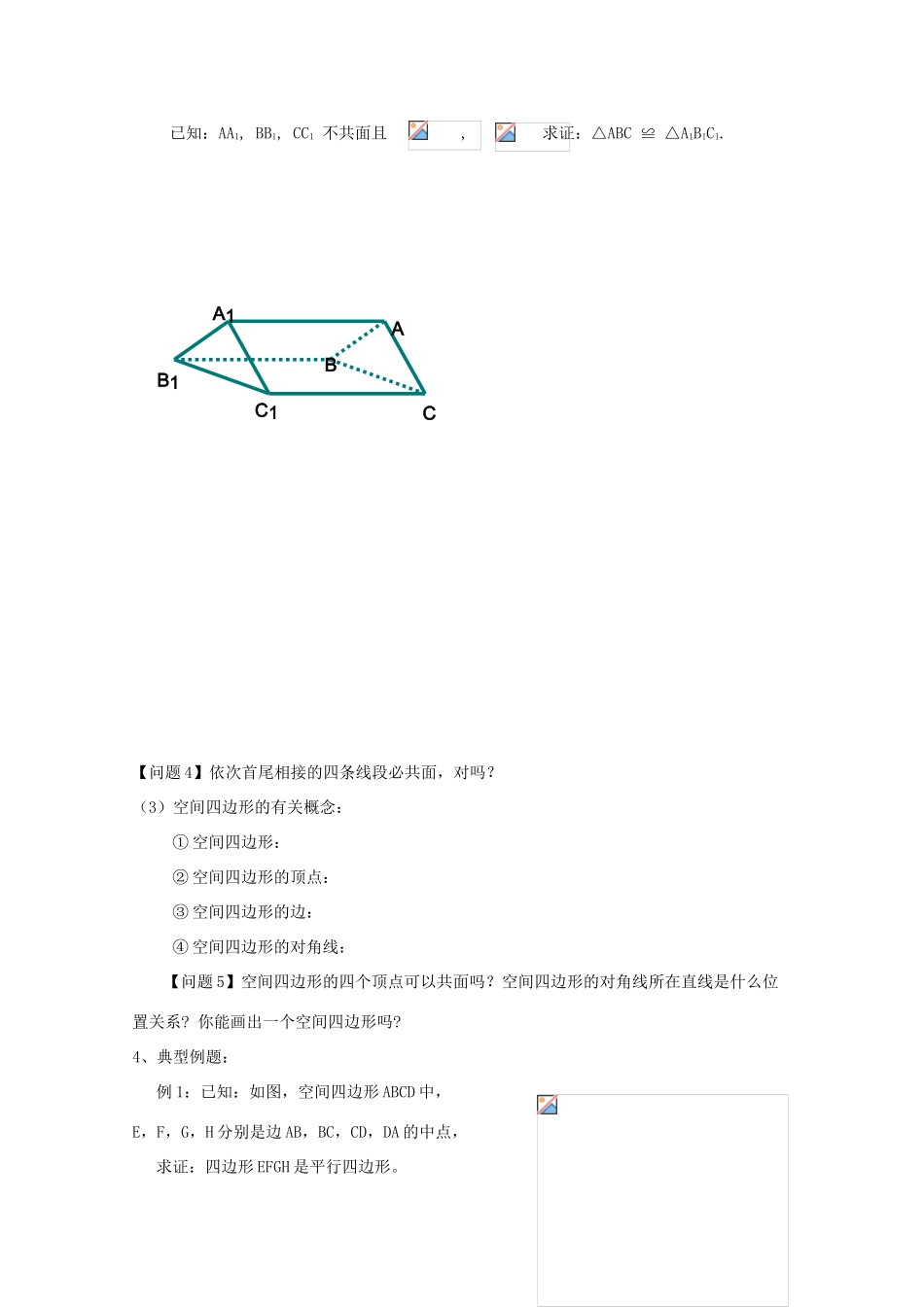
1.2.2 空间中的平行关系(线线平行) 一、课标导航:1.认识和理解空间平行线的传递性;2.会证明和应用空间等角定理3.初步了解空间四边形及其画法二、重点、难点:重点:理解空间平行线的传递性、等角定理难点:等角定理的证明三、教学过程:1、情境导入:请同学们观察我手中的三棱柱或教室的墙角线,思考一下空间中两条直线的位置关系有哪些?能否举例说明?2、初中知识回顾:(1)平行线的定义:能否说空间中无公共点的两条直线是平行直线?(2)平行公理:3、形成新知:【问题 1】在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线的位置关系如何?这一性质能推广到空间中吗?试举例说明(1)基本性质 4:小试牛刀:① 在长方体 ABCD-A1B1C1D1中, E、F 分别为 B1D1和 D1B 的中点,长方体的各棱中与 EF 平行的直线的条数有_ _条。② 判断正误:空间四条直线,如果 a∥b,c∥d,且 a∥d,那么 b∥c.【问题 2】在同一个平面内,如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角的大小关系如何?你还记得如何证明吗?这一结论能推广到空间中吗?已知:D1C1B1A1DCBAacbFE求证:证明: 【问题 1、证明两角相等的常用方法有哪些?问题 2、证明三角形全等的方法有哪些?通过这两个问题分解难度,突破难点。】(2)等角定理: 思考与讨论:(借助同学们手中的笔或纸棒,小组讨论)如果一个角的两边与另一个角的两边分别对应平行,那么这两个角的关系又如何呢?结论:【问题 3】空间中,如果∠ABC=∠A1B1C1,且 AB∥A1B1,则 BC∥B1C1对吗?小试牛刀:已知:AA1, BB1, CC1 不共面且 , 求证:△ABC ≌ △A1B1C1. 【问题 4】依次首尾相接的四条线段必共面,对吗?(3)空间四边形的有关概念:① 空间四边形:② 空间四边形的顶点:③ 空间四边形的边:④ 空间四边形的对角线:【问题 5】空间四边形的四个顶点可以共面吗?空间四边形的对角线所在直线是什么位置关系? 你能画出一个空间四边形吗?4、典型例题:例 1:已知:如图,空间四边形 ABCD 中,E,F,G,H 分别是边 AB,BC,CD,DA 的中点,求证:四边形 EFGH 是平行四边形。 AA1BB1CC1变式 1: 若在例题中添加一个条件:对角线 AC=BD,则四边形 EFGH 是什么图形?变式 2:空间四边形 ABCD 中,E,H 分别是 AB,AD 的中点,F,G 分别是 CB,CD 上的点,且 ,则四边形 EFGH 是什么图形?5、反馈练习:...