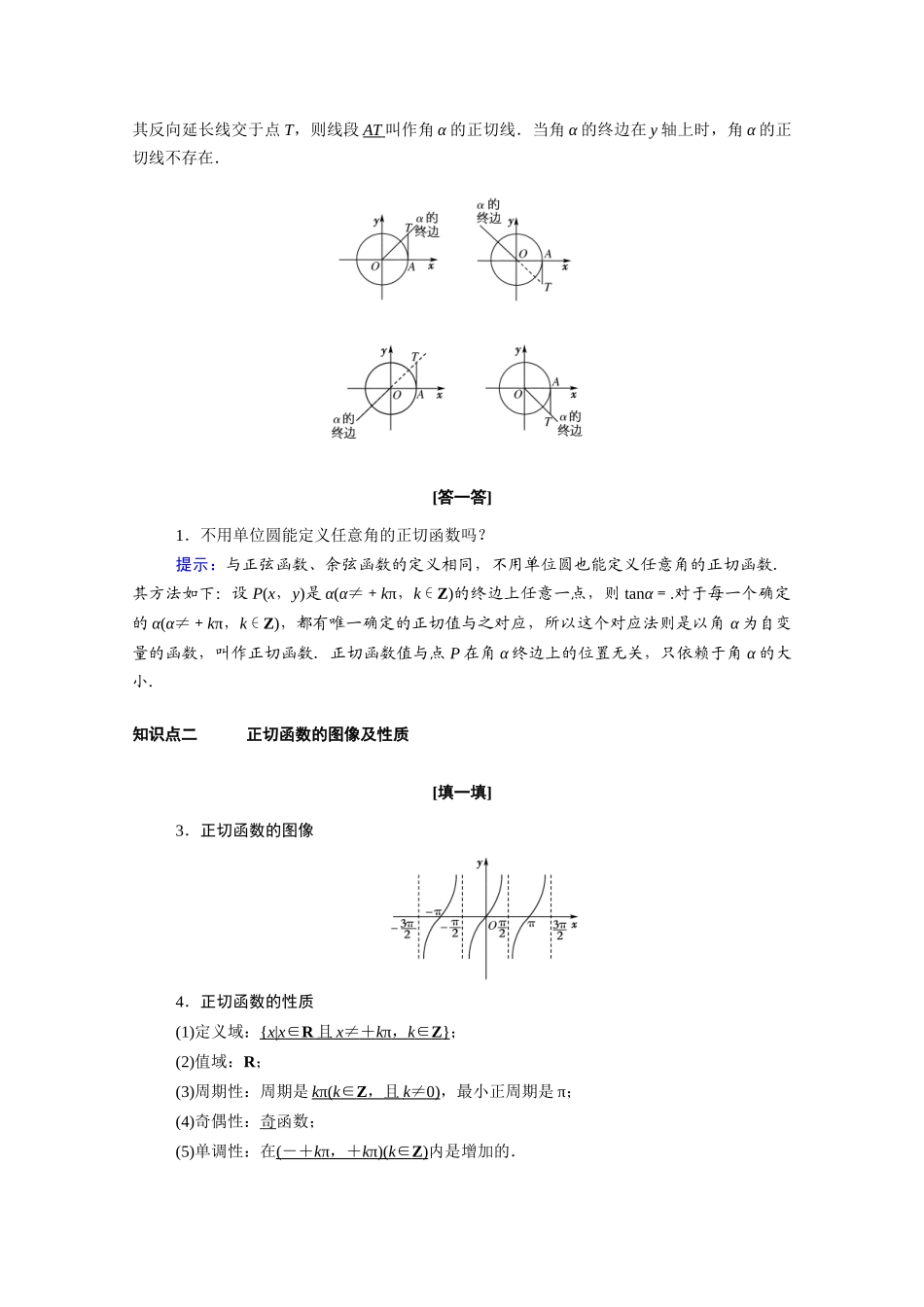
§7 正切函数7.1 正切函数的定义7.2 正切函数的图像与性质知识点一 任意角的正切函数及正切线 [填一填]1.任意角的正切函数(1)正切函数的定义在直角坐标系中(如图),如果角 α 满足:α∈R 且 α≠+kπ(k∈Z),那么,角 α 的终边与单位圆交于点 P(a,b),比值是角 α 的函数,叫作角 α 的正切函数,记作 y=tanα,其中α∈R,且 α≠+kπ(k∈Z).(2)正切函数与正弦、余弦函数的关系=tan α (α∈R,α≠+kπ,k∈Z).(3)正切函数值在各象限的符号当角在第一和第三象限时,其正切函数值为正;当角在第二和第四象限时,其正切函数值为负.2.正切线如图所示,单位圆与 x 轴的正半轴交于点 A,过点 A 作 x 轴的垂线 AT,与角 α 的终边或其反向延长线交于点 T,则线段 AT 叫作角 α 的正切线.当角 α 的终边在 y 轴上时,角 α 的正切线不存在.[答一答]1.不用单位圆能定义任意角的正切函数吗?提示:与正弦函数、余弦函数的定义相同,不用单位圆也能定义任意角的正切函数.其方法如下:设 P(x,y)是 α(α≠+kπ,k∈Z)的终边上任意一点,则 tanα=.对于每一个确定的 α(α≠+kπ,k∈Z),都有唯一确定的正切值与之对应,所以这个对应法则是以角 α 为自变量的函数,叫作正切函数.正切函数值与点 P 在角 α 终边上的位置无关,只依赖于角 α 的大小.知识点二 正切函数的图像及性质 [填一填]3.正切函数的图像4.正切函数的性质(1)定义域:{ x | x ∈ R 且 x ≠ + k π , k ∈ Z } ;(2)值域:R;(3)周期性:周期是 k π( k ∈ Z ,且 k ≠ 0) ,最小正周期是 π;(4)奇偶性:奇函数;(5)单调性:在( -+ k π ,+ k π)( k ∈ Z ) 内是增加的.(6)对称性:正切函数的图象关于原点对称,正切曲线都是中心对称图形,其对称中心坐标是( , 0)( k ∈ Z ) ,正切函数无对称轴.[答一答]2.如何作出正切函数的图像?提示:(1)几何法利用单位圆中的正切线作出正切函数图像,该方法作图较为精确,但画图时较烦琐.(2)“三点两线”法“三点”是指(-,-1),(0,0),(,1);“两线”是指 x=-和 x=.在“三点”、“两线”确定的情况下,类似于五点法作图,可大致画出正切函数在(-,)上的简图,然后向右、向左延伸即可得到正切曲线.1.用单位圆上的正切线画正切函数图像(1)建立平面直角坐标系,在 x 轴的负半轴上任取一点 O...