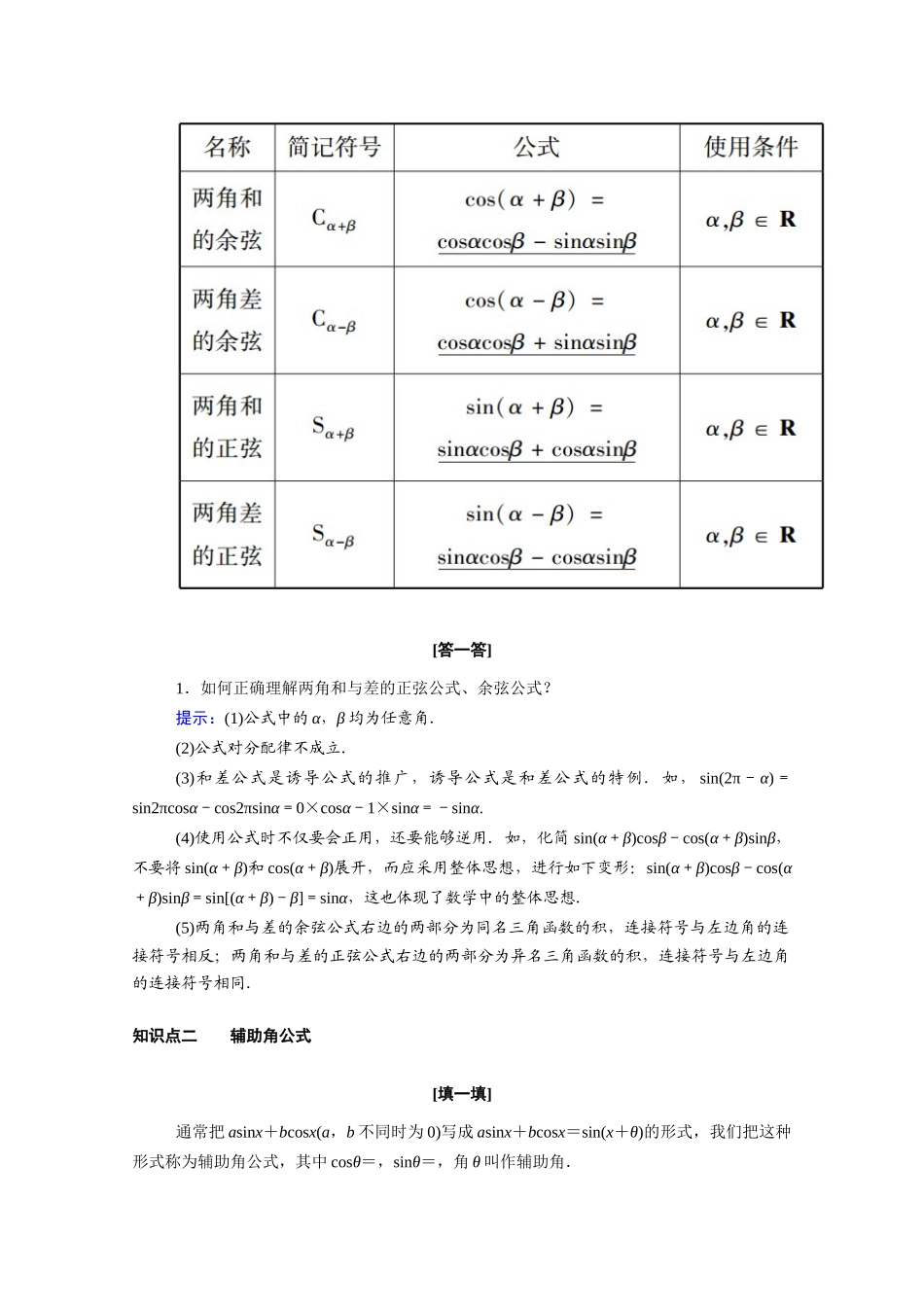
§2 两角和与差的三角函数2.1 两角差的余弦函数2.2 两角和与差的正弦、余弦函数知识点一 两角和与差的余弦公式、正弦公式 [填一填][答一答]1.如何正确理解两角和与差的正弦公式、余弦公式?提示:(1)公式中的 α,β 均为任意角.(2)公式对分配律不成立.(3)和差公式是诱导公式的推广,诱导公式是和差公式的特例.如, sin(2π-α)=sin2πcosα-cos2πsinα=0×cosα-1×sinα=-sinα.(4)使用公式时不仅要会正用,还要能够逆用.如,化简 sin(α+β)cosβ-cos(α+β)sinβ,不要将 sin(α+β)和 cos(α+β)展开,而应采用整体思想,进行如下变形:sin(α+β)cosβ-cos(α+β)sinβ=sin[(α+β)-β]=sinα,这也体现了数学中的整体思想.(5)两角和与差的余弦公式右边的两部分为同名三角函数的积,连接符号与左边角的连接符号相反;两角和与差的正弦公式右边的两部分为异名三角函数的积,连接符号与左边角的连接符号相同.知识点二 辅助角公式 [填一填]通常把 asinx+bcosx(a,b 不同时为 0)写成 asinx+bcosx=sin(x+θ)的形式,我们把这种形式称为辅助角公式,其中 cosθ=,sinθ=,角 θ 叫作辅助角.[答一答]2.如何化简 asinα+bcosα(ab≠0)?提示:逆用两角和与差的正弦公式,凑出 sinαcosβ±cosαsinβ 的形式来化简.asinα+bcosα=(sinα+cosα). ()2+()2=1,∴可设 cosθ=,sinθ=,则 tanθ=(θ 称为辅助角).∴asinα+bcosα=(sinαcosθ+cosαsinθ)=sin(α+θ).特别是当=±1,±,±时,θ 是特殊角.例如,3sinα-3cosα=(sinα-cosα)=6(sinα-cosα)=6(sinαcos-cosαsin)=6sin(α-).1.对公式 Cα±β的两点说明(1)公式的结构特点公式的左边是和(差)角的余弦,右边的式子是含有同名函数之积的差(和)式,可用口诀“余余正正号相反”记忆公式.(2)公式的适用条件公式中的 α,β 不仅可以是任意具体的角,也可以是一个“团体”如 cos(-)中的“”相当于公式中的角“α”,“”相当于公式中的角“β”.因此对公式的理解要注意结构形式,而不要局限于具体的角. 3.注意公式的结构特征和符号规律对于公式 Cα-β,Cα+β,可记为“同名相乘,符号反”.对于公式 Sα-β,Sα+β,可记为“异名相乘,符号同”. 类型一 利用公式求值 【例 1】 求值:(1)sin43°cos13°-sin13°sin47°;(2)cos(α-35°)·cos(25°+α)+sin(α...