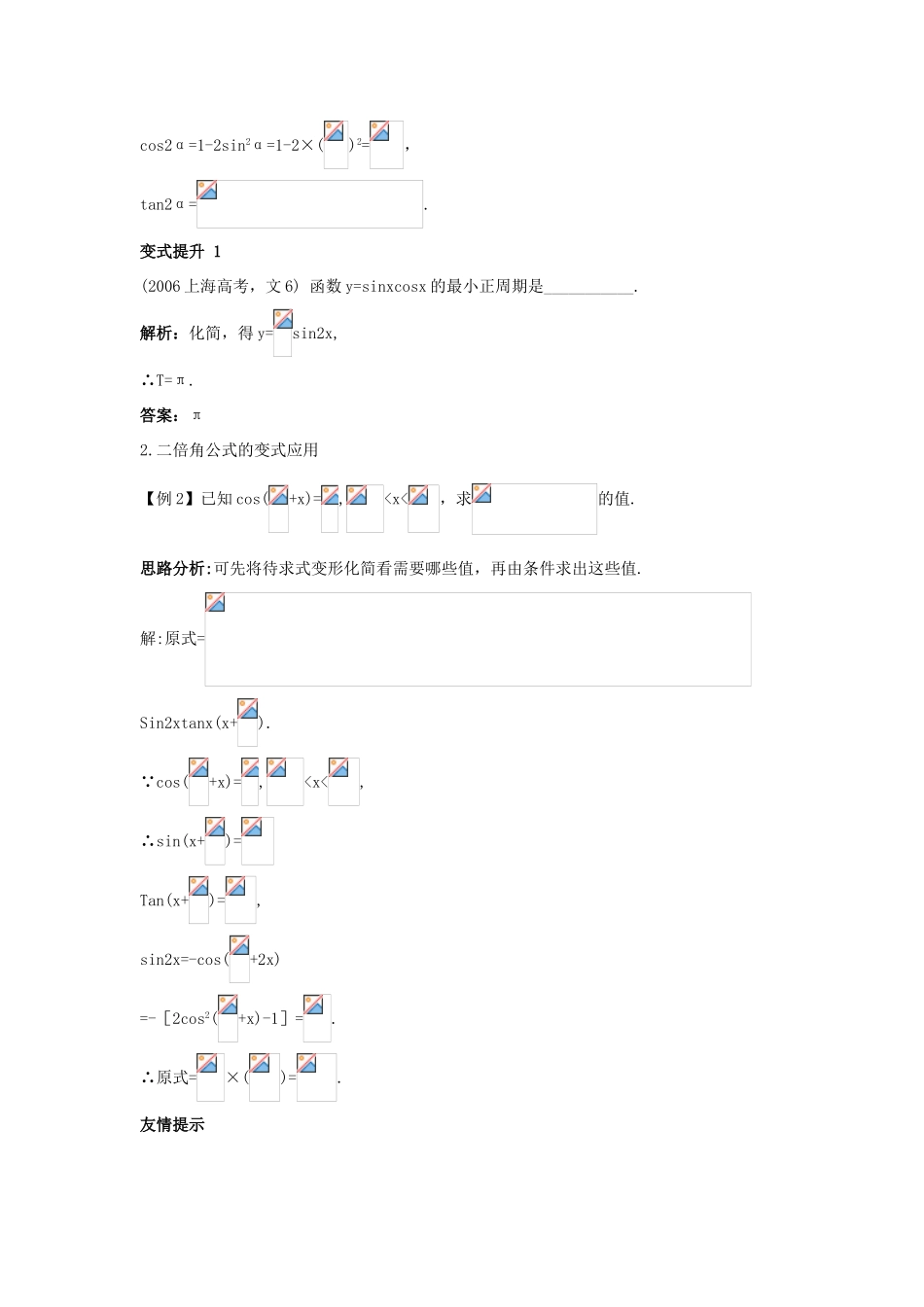
3.3 二倍角的正弦、余弦和正切课堂导学三点剖析1.二倍角与降幂公式【例 1】 已知 sin(+x)sin(-x)=,x∈(,π),求 sin4x 的值.思路分析:注意到+x+-x=,可用诱导公式变形后计算.解:由 sin(+x)sin(-x)=可得sin(+x)cos(+x)=,即sin(+2x)=,∴sin(+2x)=,即 cos2x=.又∵x∈(,π),∴2x∈(π,2π).∴sin2x=.∴sin4x=2sin2xcos2x=.友情提示 在应用二倍角的同时,也用诱导公式或同角的三角函数关系.各个击破类题演练 1已知 sinα=,α∈(,π),求 sin2α,cos2α,tan2α 的值.解析:∵sinα=,α∈(,π),∴cosα=,∴sin2α=2sinαcosα=2××()=,cos2α=1-2sin2α=1-2×()2=,tan2α=.变式提升 1(2006 上海高考,文 6) 函数 y=sinxcosx 的最小正周期是___________.解析:化简,得 y=sin2x,∴T=π.答案:π2.二倍角公式的变式应用【例 2】已知 cos(+x)=,