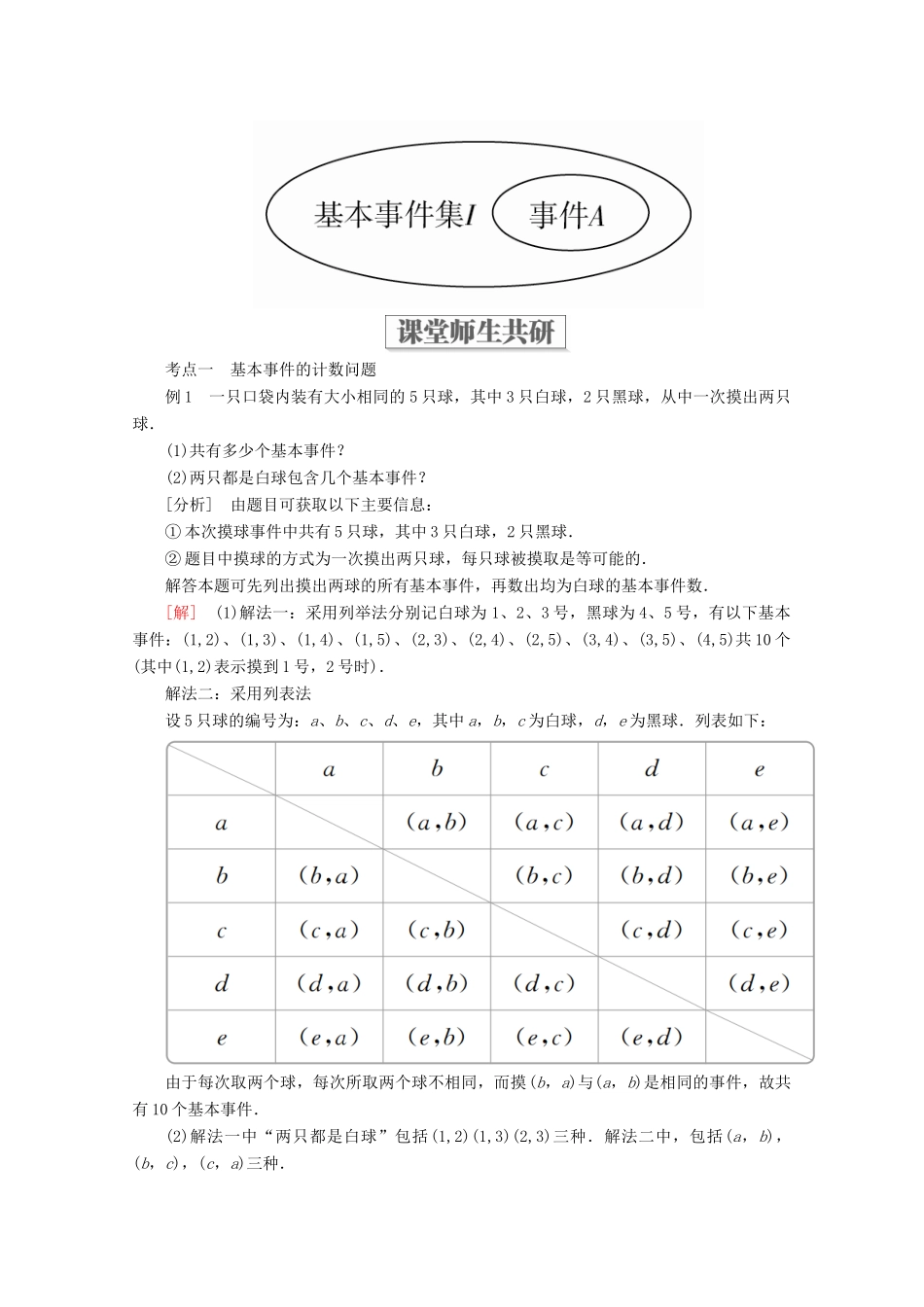
3.2.1 古典概型的特征和概率计算公式 3.2.2 建立概率模型[航向标·学习目标]1.理解古典概型的两个基本特征.2.掌握古典概型的概念及概率的计算公式.[读教材·自主学习]1.基本事件:一次试验中可能出现的□ 每一个结果 称为一个基本事件.2.基本事件的特点:(1)任何两个基本事件是不可能同时发生的.一次试验中,只可能出现一种结果,即出现一个基本事件.(2)任何事件都可以表示成基本事件的和.3.古典概型:(1)试验的所有可能结果只有□ 有限个 ,每次试验只出现其中的一个结果.(2)每一个试验结果出现的可能性□ 相同. 我们把具有这样两个特征的随机试验的数学模型称为古典概型.4.古典概型的计算公式:对于古典概型,通常试验中的某一事件 A 是由几个基本事件组成,如果试验的所有可能结果(基本事件)数为 n,随机事件 A 包含的基本事件数为 m,那么事件 A 的概率规定为□P(A)=.[看名师·疑难剖析]1.古典概型试验有两个共同的特征(1)有限性:在一次试验中,可能出现的结果是有限个,即只有有限个不同的基本事件.(2)等可能性:每个基本事件发生的可能性是均等的.2.古典概型的概率公式(等可能性事件的概率)(1)若试验的结果是由 n 个基本事件组成,并且每个基本事件的发生是等可能的,而随机事件 A 包含的基本事件数为 m,则由互斥事件的概率加法公式可得:所以古典概型中,P(A)=. 这就是概率的古典定义.(2)用集合观点来理解事件 A 与基本事件的关系(如下图):在一次试验中,等可能出现 n个结果组成一个集合 I,这 n 个结果就是集合 I 的 n 个元素,各基本事件均对应于集合 I 的含有 1 个元素的子集,包含每个结果的事件 A 对应于 I 的含有 m 个元素的子集 A.因此从集合的角度看,事件 A 的概率是子集 A 的元素个数(记作 card(A))与集合 I 的元素个数(记作card(I))的比值,即 P(A)==.考点一 基本事件的计数问题例 1 一只口袋内装有大小相同的 5 只球,其中 3 只白球,2 只黑球,从中一次摸出两只球.(1)共有多少个基本事件?(2)两只都是白球包含几个基本事件?[分析] 由题目可获取以下主要信息:① 本次摸球事件中共有 5 只球,其中 3 只白球,2 只黑球.② 题目中摸球的方式为一次摸出两只球,每只球被摸取是等可能的.解答本题可先列出摸出两球的所有基本事件,再数出均为白球的基本事件数.[解] (1)解法一:采用列举法分别记白球为 1、2、3 号,黑球为...