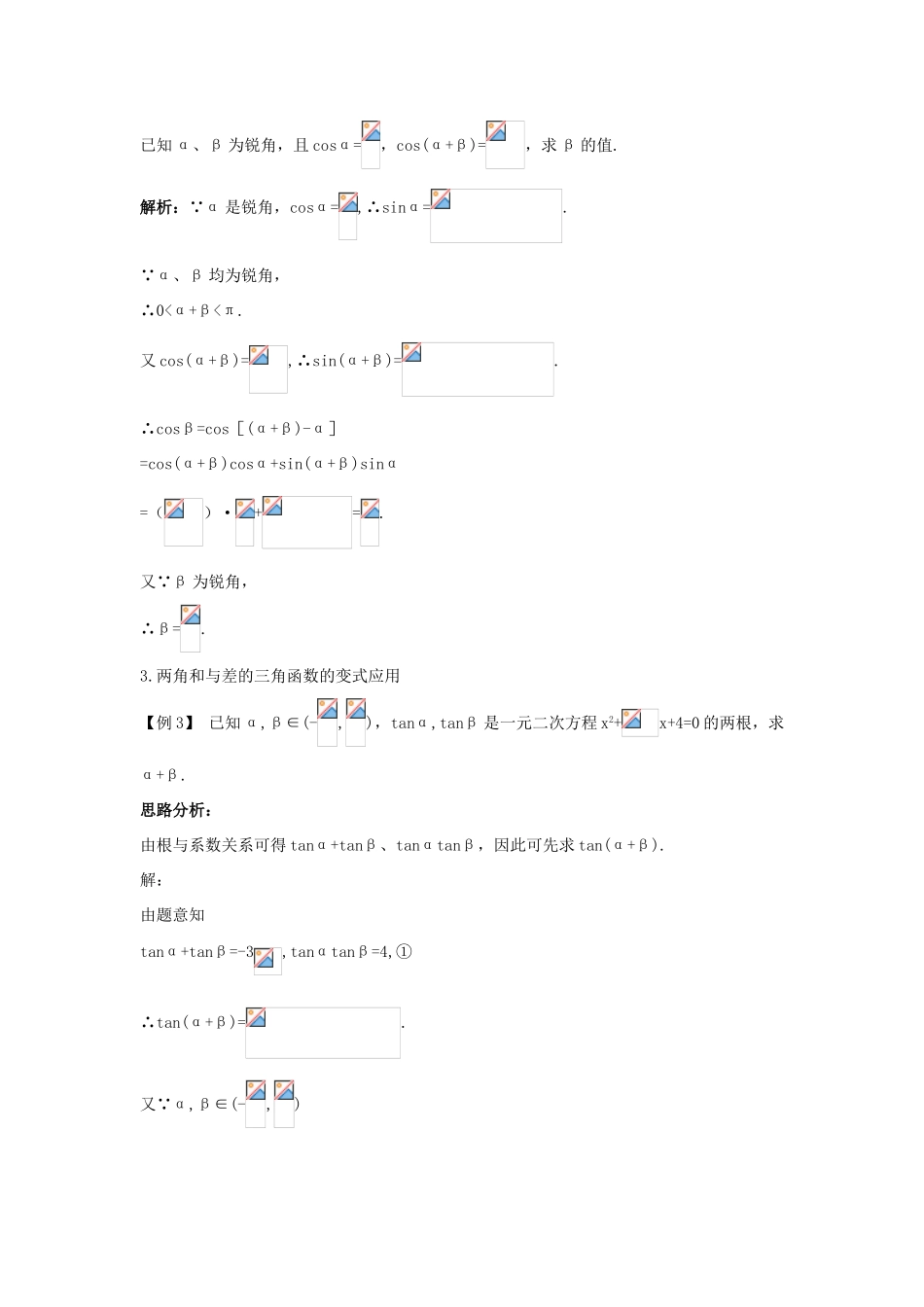
3.2 两角和与差的三角函数课堂导学三点剖析1.两角和与差的三角函数公式的简单运用【例 1】 若 sinα=,sinβ=且 α、β 是锐角,求 α+β 的值.思路分析:可先求出 α+β 的某种三角函数值,然后再确定 α+β 的值.解:∵α、β 是锐角,∴cosα=,cosβ=.∴sin(α+β)=sinαcosβ+cosαsinβ=.又∵sinα=<,sinβ=<,∴0°<α<30°,0°<β<30°.∴0°<α+β<60°.∴α+β=45°.各个击破类题演练 1计算 sin33°cos27°+sin57°cos63°的值.解析:原式=sin33°cos27°+cos33°sin27°=sin(33°+27°)=sin60°=,或:原式=cos57°cos27°+sin57°sin27°=cos(57°-27°)=cos30°=.变式提升 1sin163°sin223°+sin253°sin313°=___________.解析:原式=sin(180°-17°)·sin(180°+43°)+sin(270°-17°)+sin(270°+43°)=-sin17°sin43°+cos17°cos43°=cos(17°+43°)=cos60°=.答案:2.两角差的余弦公式的运用【例 2】 已知 cos(α+β)=,cos(α-β)=,求 tanαtanβ 的值.思路分析:题目中要求的是单角 α 与 β 的函数值,所以自然要想到用和差公式分解,然后用商式求解.解:由①+② 得 cosαcosβ=,②-① 得 sinαsinβ=,∴tanαtanβ==.友情提示 在利用两角和差公式的同时,运用同角三角函数关系,把不同类型的公式放在一起使用是本章题目的特点.类题演练 2设 a∈(0,),若 sinα=,则cos(α+)等于( )A. B. C. D.-解析:∵α∈(0,),sinα=,∴cosα=,又cos(α+)=(cosα·cos-sinα·sin)=cosα-sinα=.答案:B变式提升 2已知 α、β 为锐角,且 cosα=,cos(α+β)=,求 β 的值.解析:∵α 是锐角,cosα=,∴sinα=.∵α、β 均为锐角,∴0<α+β<π.又 cos(α+β)=,∴sin(α+β)=.∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=()·+=.又∵β 为锐角,∴β=.3.两角和与差的三角函数的变式应用【例 3】 已知 α,β∈(-,),tanα,tanβ 是一元二次方程 x2+x+4=0 的两根,求 α+β.思路分析:由根与系数关系可得 tanα+tanβ、tanαtanβ,因此可先求 tan(α+β).解:由题意知tanα+tanβ=-3,tanαtanβ=4,①∴tan(α+β)=.又∵α,β∈(-,)且由①知 α∈(-,0),β∈(-,0),∴α+β∈(-π,0).∴α+β=.类题演练 3计算 tan10°+tan50°+tan10°tan50°的值.解析:原式=tan(10°+50°)(1-tan10°tan50°)+tan10°tan50°=(1-tan10°tan50°)+tan10°tan50°=.变式提升 3求值:tan10°tan20°+tan20°tan60°+tan60°tan10°.解析:原式=tan10°tan20°+(tan10°+tan20°)=tan10°tan20°+tan30°(1-tan10°tan20°)=1.