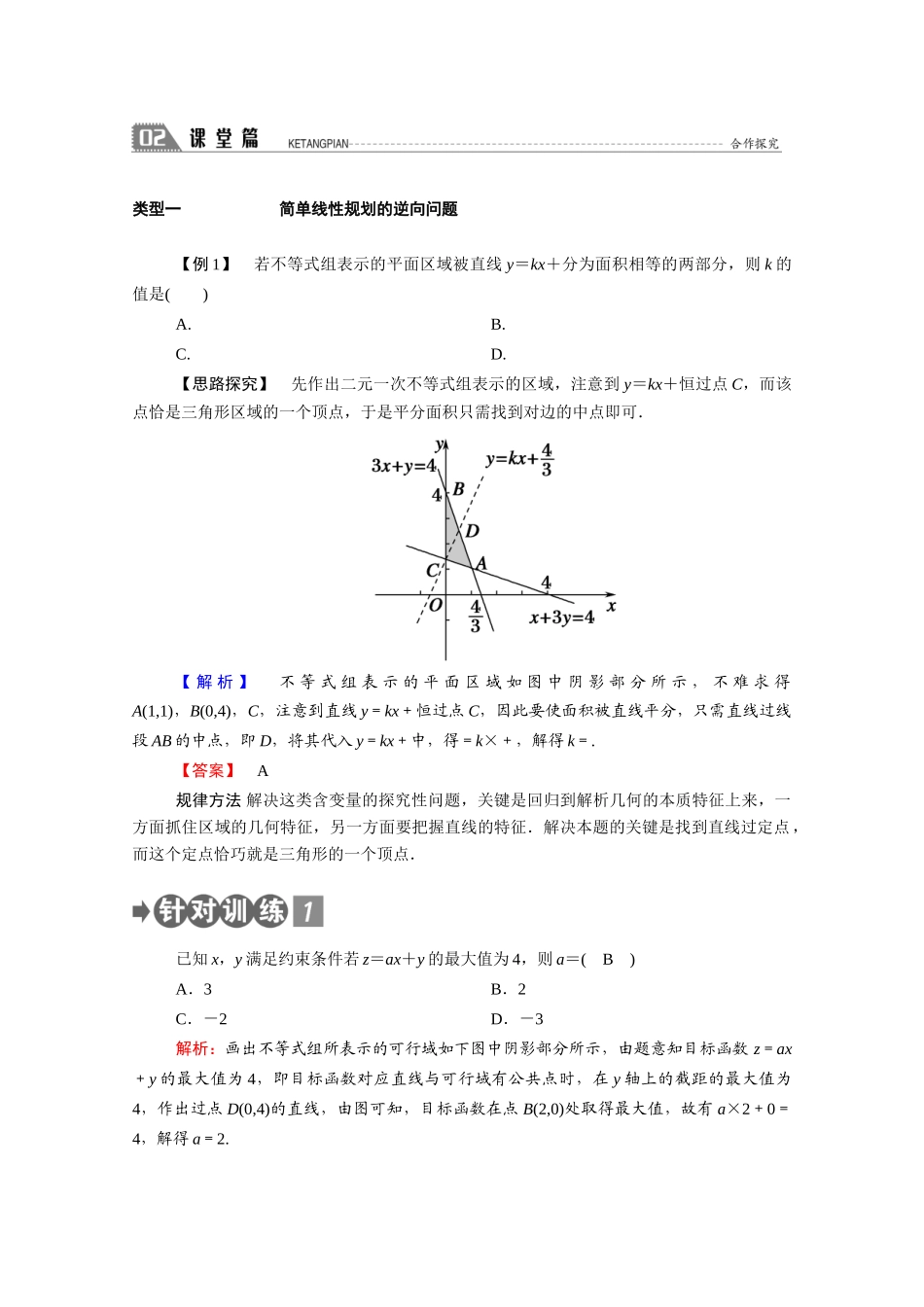
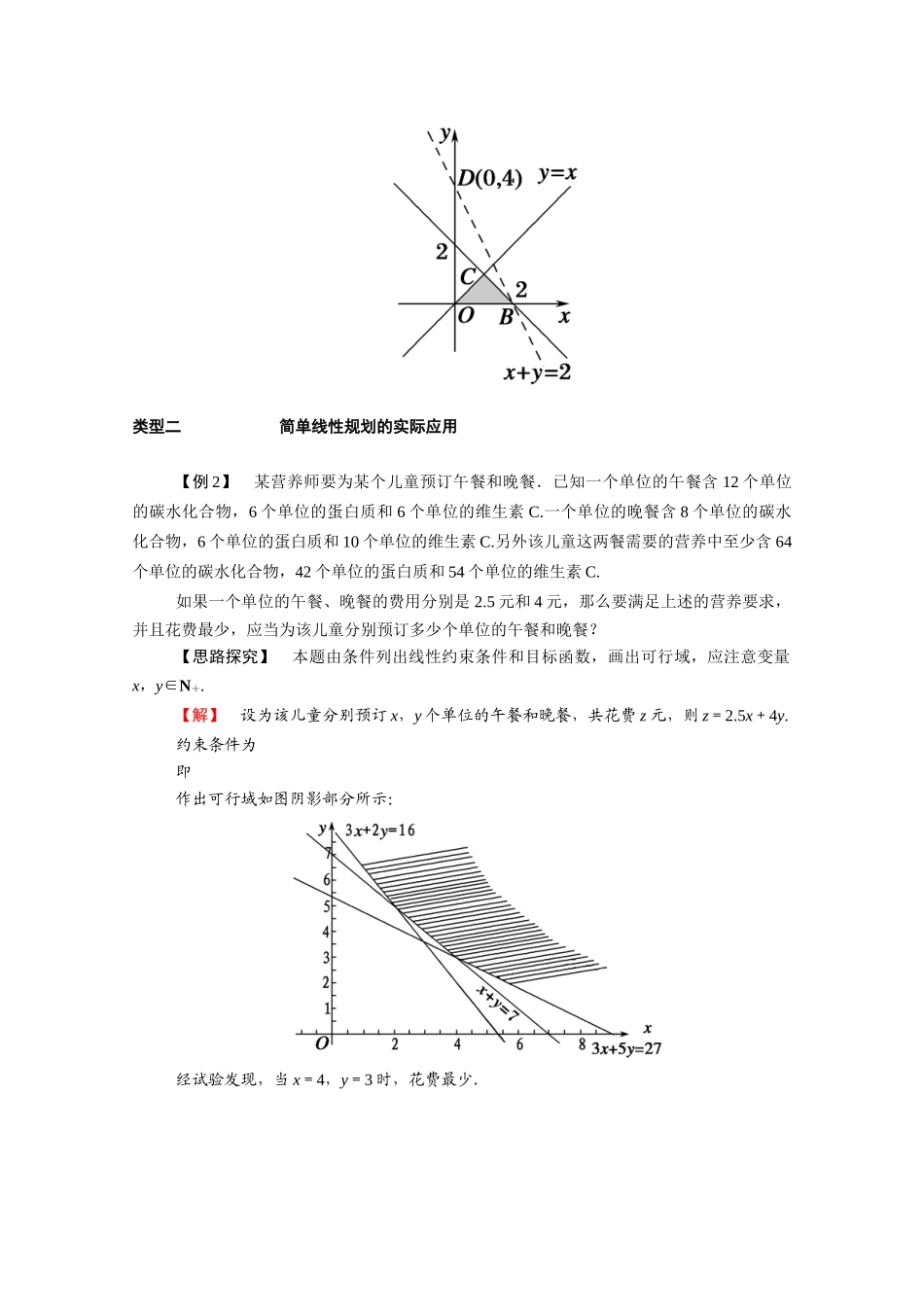
4.3 简单线性规划的应用知识点 解决线性规划的步骤 [填一填]在约束条件下,求目标函数 z=ax+by+c 的最小值或最大值的求解步骤为:(1)作出可行域;(2)作出直线 l0:ax + by = 0 ;(3)确定 l0的平移方向,依可行域判断取得最优解的点;(4)解相关方程组,求出最优解,从而得出目标函数的最小值或最大值.[答一答]解答线性规划应用题的关键是什么?提示:关键是将实际问题转化为数学问题,即找出约束条件和目标函数.解答线性规划应用题的注意事项(1)在线性规划问题的应用中,常常是题中的条件较多,因此认真审题非常重要;(2)线性约束条件中有无等号要依据条件加以判断;(3)结合实际问题,未知数 x,y 等是否有限制,如 x,y 为正整数,非负数等;(4)分清线性约束条件和线性目标函数,线性约束条件一般是不等式,而线性目标函数却是一个等式;(5)图对解决线性规划问题至关重要,关键步骤基本上都是在图上完成的,所以作图应尽可能地准确,图上操作尽可能规范.但作图中必然会有误差,假如图上的最优点并不明显易辨时,需将几个有可能是最优点的坐标都求出来,然后逐一检查,以确定最优解.类型一 简单线性规划的逆向问题 【例 1】 若不等式组表示的平面区域被直线 y=kx+分为面积相等的两部分,则 k 的值是( )A.B.C.D.【思路探究】 先作出二元一次不等式组表示的区域,注意到 y=kx+恒过点 C,而该点恰是三角形区域的一个顶点,于是平分面积只需找到对边的中点即可.【 解 析 】 不 等 式 组 表 示 的 平 面 区 域 如 图 中 阴 影 部 分 所 示 , 不 难 求 得A(1,1),B(0,4),C,注意到直线 y=kx+恒过点 C,因此要使面积被直线平分,只需直线过线段 AB 的中点,即 D,将其代入 y=kx+中,得=k×+,解得 k=.【答案】 A规律方法 解决这类含变量的探究性问题,关键是回归到解析几何的本质特征上来,一方面抓住区域的几何特征,另一方面要把握直线的特征.解决本题的关键是找到直线过定点,而这个定点恰巧就是三角形的一个顶点.已知 x,y 满足约束条件若 z=ax+y 的最大值为 4,则 a=( B )A.3 B.2C.-2 D.-3解析:画出不等式组所表示的可行域如下图中阴影部分所示,由题意知目标函数 z=ax+y 的最大值为 4,即目标函数对应直线与可行域有公共点时,在 y 轴上的截距的最大值为4,作出过点 D(0,4)的直线,由图可知,目标函数在点 B(2,0)处取得最...