第十一讲--复合型准则

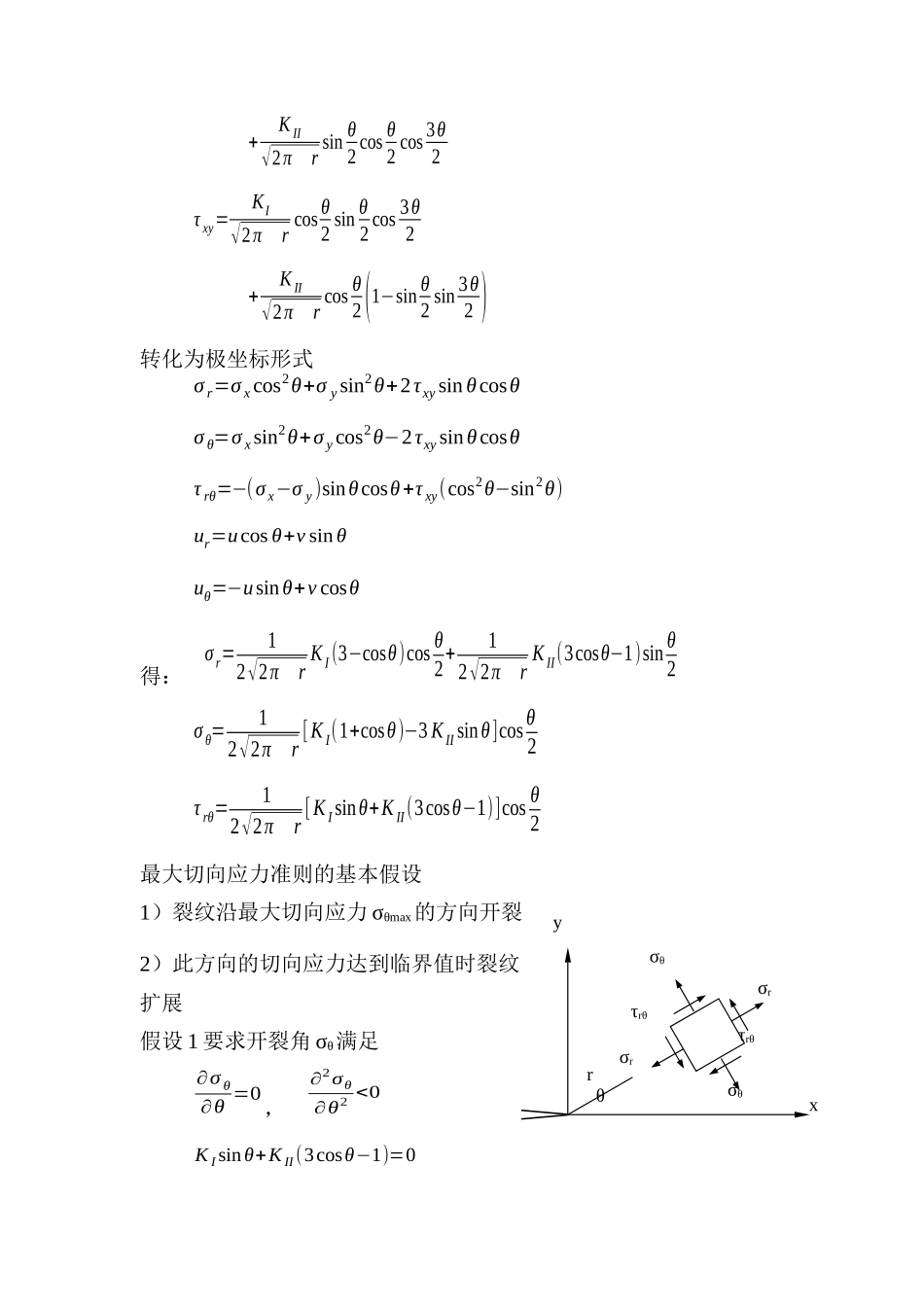
第十一讲 复合型准则上节概述裂纹的类型G 准则，K 准则，应力强度因子和能量释放率的关系裂纹尖端应力场、位移场裂纹尖端塑性区，线弹性断裂力学应用于小范围屈服其它裂纹形式的应力强度因子实际的裂纹往往是张开型和滑移型（I、II）并存或张开型和撕开型（I、III）并存。Irwin 断裂准则不能简单地用于复合型裂纹问题（Irwin 的 K 准则理论假定裂纹按原方向开裂）1）I、III 型裂纹一般按原方向开裂2）II 型裂纹一般不按原方向开裂3）复合型裂纹一般不按原方向开裂复合型裂纹要解决的问题1）裂纹沿什么方向开裂2）裂纹在什么条件下开裂1．最大切向应力准则（Erdogan and Sih, 1963）I、II 复合型裂纹尖端应力场 σ x=KI√2 π rcos θ2(1−sin θ2 sin 3θ2 ) −K II√2 π rsin θ2(2+cos θ2 cos 3θ2 ) σ y=KI√2π rcos θ2(1+sin θ2 sin 3θ2 )2arxy +K II√2π rsin θ2 cos θ2 cos 3θ2 τ xy=KI√2π rcos θ2 sin θ2 cos 3θ2 +K II√2π rcos θ2(1−sin θ2 sin 3θ2 )转化为极坐标形式 σ r=σ xcos2θ+σ ysin2θ+2τxy sinθcosθ σ θ=σ xsin2θ+σ ycos2θ−2τxy sinθcosθ τ rθ=−(σ x−σ y)sinθcosθ+τ xy(cos2θ−sin2θ) ur=ucos θ+v sin θ uθ=−usinθ+v cosθ得： σ r=12√2π rK I(3−cosθ)cos θ2+12√2π rK II(3cosθ−1)sin θ2 σ θ=12√2π r[K I(1+cosθ)−3 K II sinθ]cos θ2 τ rθ=12√2π r[K Isinθ+K II(3cosθ−1)]cos θ2最大切向应力准则的基本假设1）裂纹沿最大切向应力 σθmax的方向开裂2）此方向的切向应力达到临界值时裂纹扩展假设 1 要求开裂角 σθ满足 ∂σ θ∂θ =0， ∂2σθ∂θ2 <0 K I sinθ+K II(3cosθ−1)=0yxrθτrθτrθσθσθσrσr cosθ0=3 K II2 +√ KI4+8 KI2 K II2KI2+9K II2该方向上的切向应力 σ θ=1√2π r[K Icos2 θ02 −32 K II sinθ0]cosθ02 =Kθ√2 π rKθ：等效应力强度因子假设 2 认为切向应力达到临界值 σθC时裂纹失稳，而临界值 σθC由 I 型条件给出 Kθ=[ K I cos2 θ02 −32 K II sinθ0]cosθ02 =KIC将复合型裂纹转化为当量 I 型裂纹问题讨论1）纯 I 型，KII = 0，简化为 KI = KIC2）纯 II 型，KI = 0，开裂角 θ0 = ...