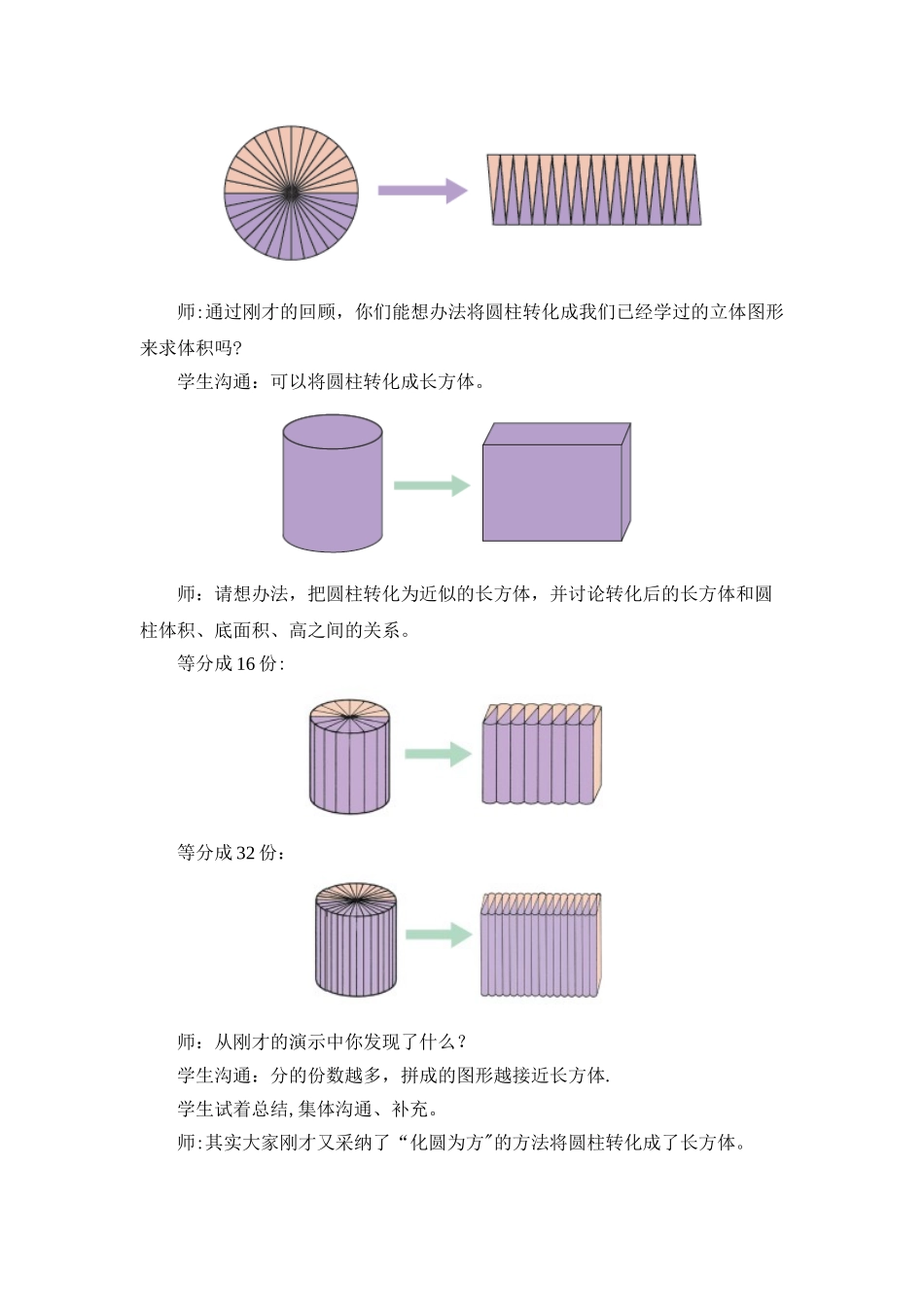
圆柱的体积教学目标1.通过切割圆柱体,拼成近似的长方体,从而推导出圆柱的体积公式这一教学过程,向学生渗透转化思想.2.通过圆柱体体积公式的推导,培育学生的分析推理能力.3.理解圆柱体体积公式的推导过程,掌握计算公式;会运用公式计算圆柱的体积。教学重、难点重点:圆柱体体积的计算。难点:灵活运用圆柱体体积的计算公式.教学准备多媒体课件。教学过程一、新课导入师:同学们,天气渐渐热了,在夏季同学们最喜爱的冷饮是什么?师:小明买了两个冰淇淋,你猜猜哪种包装盒体积大?(粗细、长短都不同)师:对,要知道它们的体积才行.二、合作探究师:怎样求圆柱的体积呢?学生思考,并沟通。师:请大家借助圆的面积公式的推导方法想一想,怎样推导出圆柱的体积公式?学生回忆圆面积公式的推导过程,并猜想圆柱体积公式的推导方法。师:通过刚才的回顾,你们能想办法将圆柱转化成我们已经学过的立体图形来求体积吗?学生沟通:可以将圆柱转化成长方体。师:请想办法,把圆柱转化为近似的长方体,并讨论转化后的长方体和圆柱体积、底面积、高之间的关系。等分成 16 份:等分成 32 份:师:从刚才的演示中你发现了什么?学生沟通:分的份数越多,拼成的图形越接近长方体.学生试着总结,集体沟通、补充。师:其实大家刚才又采纳了“化圆为方"的方法将圆柱转化成了长方体。你现在能总结出圆柱体积的计算公式吗?说一说你是怎样想的?根据学生的回答师板书:长方体的体积 = 底面积 × 高↓ ↓ ↓ 圆柱的体积 = 底面积 × 高师:假如用 V 表示体积,用 S 表示圆柱的底面积,用 h 表示高。你能用字母表示圆柱的体积公式吗?生:V=Sh师:刚才我们共同讨论出了求圆柱的体积的计算公式,你能根据公式计算圆柱形包装盒的体积是多少立方厘米吗?底面积:3。14×(12÷2)²=113.04(cm²)体积:113。04×20=2260.8(cm³)答:圆柱形包装盒的体积是 2260。8cm³。三、自主练习1.求下面图形的体积。答案:(1)3。14×3²×10=282。6(cm³)(2)3。14×(8÷2)²×8=401。92(cm³)(3)3.14×(4÷2)²×10=125.6(cm³)2.哪一根木料的体积大?答案:第一根木料:3。14×(0。4÷2)²×10=1.256(m³)第二个根木料:3。14×(0.6÷2)²×8=2。2608(m³)3.填表。答案:10,314;4,150。72四、课堂小结通过今日的学习,你收获了什么?假如有问题可以提出来,大家一起解决。五、课后作业1.2.一个圆柱形油桶,从里面量底面直径是 40 ...