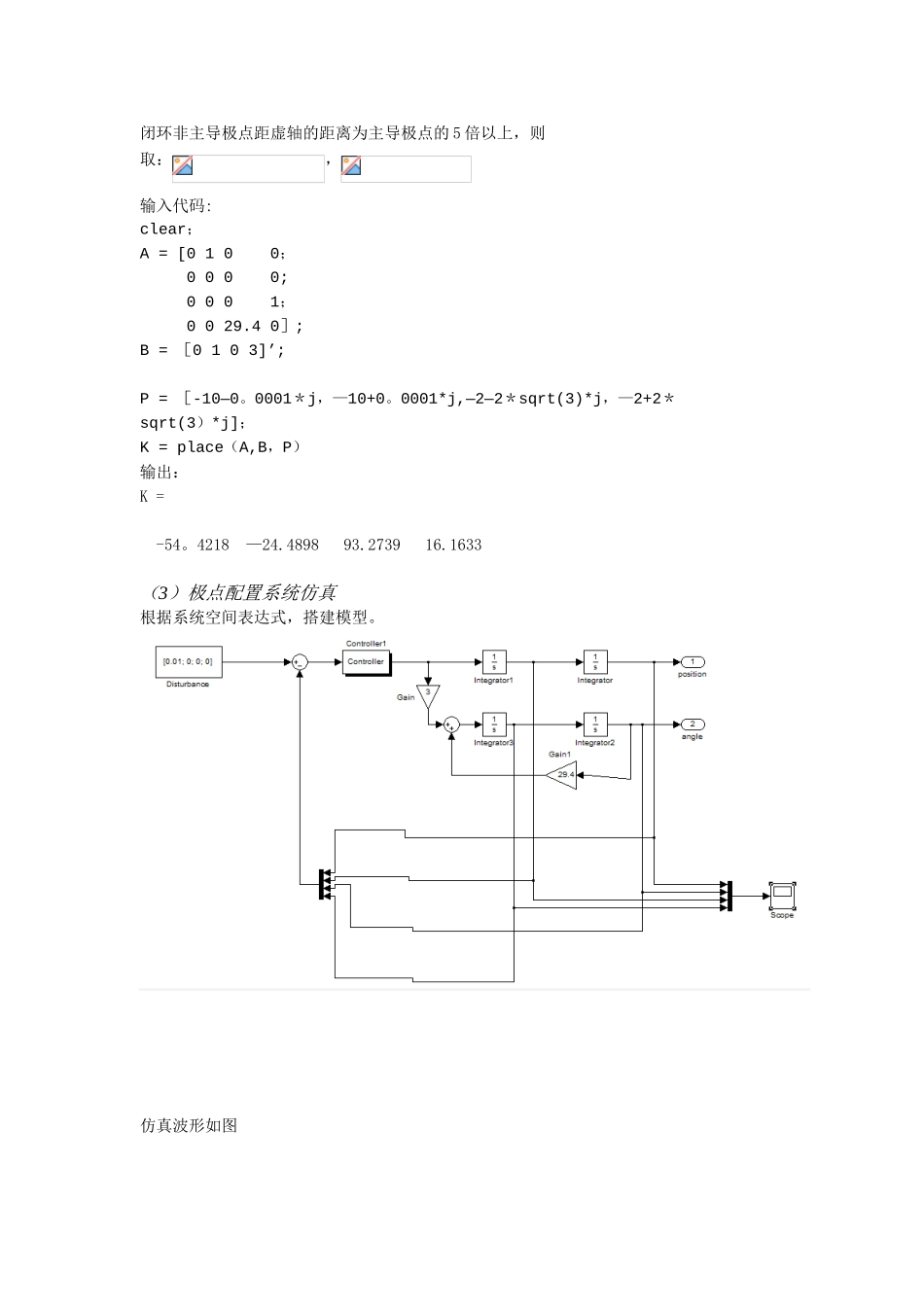
广 西 大 学 实 验 报 告实验内容:一阶倒立摆含观测器的状态反馈控制系统综合与设计 张凯强 (0902100202) 、毛世博(0902100110)、李季(0902100206) 一、实验时间:2025。3.8二、实验地点:综合楼 702三、实验目的1、理解并掌握线性状态反馈控制的原理和方法;2、理解并掌握线性观测器的设计方法;3、练习控制性能比较与评估的方法。四、实验设备与软件:1、倒立摆试验台2、MATLAB 软件五、实验原理1、被控对象模型及其线性化根据牛顿定律建立系统垂直和水平方向的动力学方程,计及 u=F,得 (1) (2)保留低阶项,项,忽略微小的高次项,在竖直位置处进行线性化。由(1)(2)得 (3) (4)令,,输入为,则状态方程为 (5)代入参数,忽略摩擦得 (6)该状态方程输入是加速度,输出是小车位置和摆杆角度。2、时不变线性连续系统的状态反馈控制与观测器对时不变线性连续系统 以系统状态为反馈变量产生控制 这种控制方式称为状态反馈控制,但状态作为系统内部变量,一般很难直接测出,为此引入状态观测器。全维状态观测器的动态方程为 若输出矩阵 C 为满秩时,可设计较简单的降维状态观测器,其最小维数为 n—m(n 代表状态个数,m 代表输出个数)。六、实验内容1、状态反馈及极点配置(1) 能控性检查:输入代码:clear;A = [0 1 0 0; 0 0 0 0; 0 0 0 1; 0 0 29.4 0];B = [0 1 0 3]';C = [1 0 0 0; 0 1 0 0];D = [0 0]';Uc = ctrb(A,B);rank(Uc)输出:ans = 4系统能控性矩阵满秩,即系统状态完全能控。(2)系统极点配置选取系统主导极点:,闭环非主导极点距虚轴的距离为主导极点的 5 倍以上,则取:,输入代码:clear;A = [0 1 0 0; 0 0 0 0; 0 0 0 1; 0 0 29.4 0];B = [0 1 0 3]’; P = [-10—0。0001*j,—10+0。0001*j,—2—2*sqrt(3)*j,—2+2*sqrt(3)*j];K = place(A,B,P)输出:K = -54。4218 —24.4898 93.2739 16.1633(3)极点配置系统仿真根据系统空间表达式,搭建模型。 仿真波形如图从仿真结果可以看出,小车最终稳定,小车速度,摆杆角度,角速度最终都稳定在 0 位置,小车位置超调≤5%,调整时间≤2s,基本符合控制要求。2、采纳状态观测器的状态反馈系统设计(1)闭环观测器极点配置 〈1> 推断可观性输入代码: A = [0 1 0 0;0 0 0 0;0 0 0 1;0 0 29.4 0];B = [0;1;0;3];C = ...