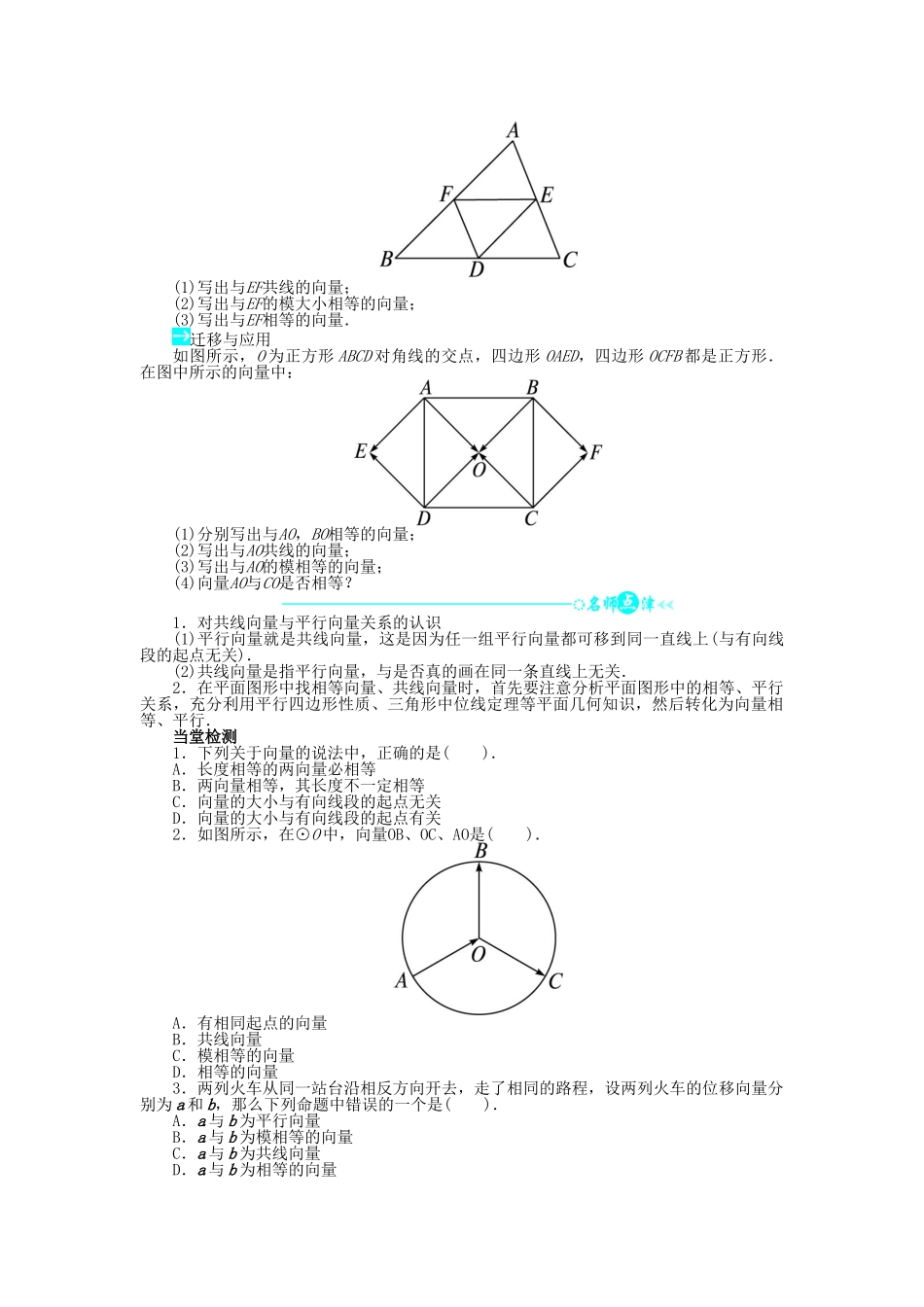
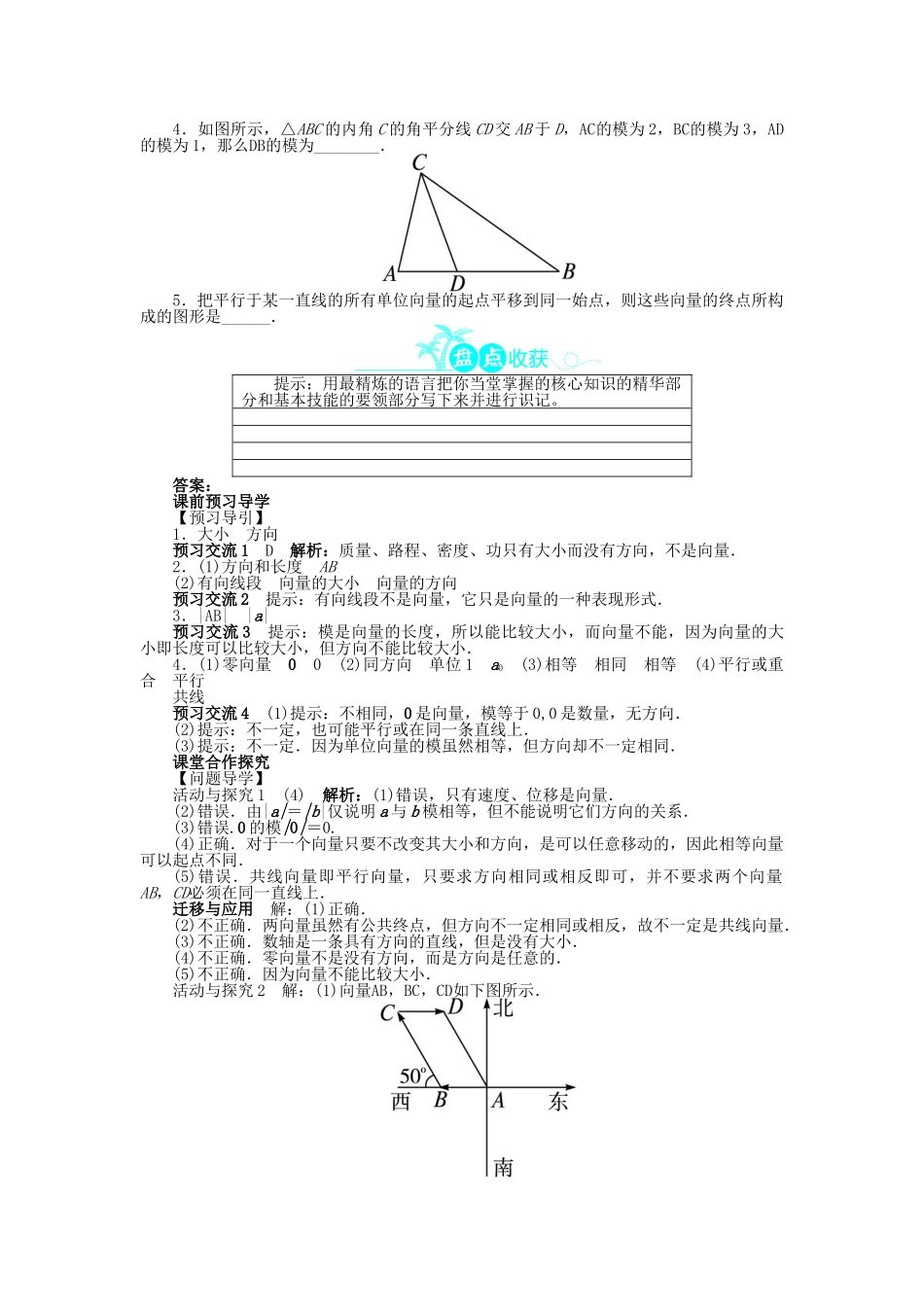
2.1 从位移、速度、力到向量问题导学1.向量的有关概念活动与探究 1给出下列几种说法:(1)温度、速度、位移这些物理量都是向量;(2)若|a|=|b|,则 a=b 或 a=-b;(3)向量的模一定是正数;(4)起点不同,但方向相同且模相等的几个向量是相等向量;(5)向量AB与CD是共线向量,则 A,B,C,D 四点必在同一直线上.其中正确的序号是________.迁移与应用判断下列说法是否正确,并说明理由.(1)向量AB与向量BA的模相等;(2)两个有公共终点的向量,一定是共线向量;(3)数轴是向量;(4)零向量没有方向;(5)若向量 a 与 b 同向,且|a|>|b|,则 a>b.关于向量有关概念的几点说明:(1)向量不同于数量,数量可以比较大小,而向量由模和方向确定,方向不能比较大小,因此向量也不能比较大小.(2)数学上所研究的向量是自由向量,可以平移,因此向量中的共线与平行是相同的,而直线或线段中的共线与平行是不同的.(3)零向量是特殊向量,方向可以看作是任意的.2.向量的表示方法活动与探究 2一运输汽车从 A 点出发向西行驶了 100 km 到达 B 点,然后又改变方向向西偏北 50°走了 200 km 到达 C 点,最后又改变方向,向东行驶了 100 km 到达 D 点.(1)作出向量AB,BC,CD;(2)求AD.迁移与应用在如图所示的坐标系中(1 个小方格表示 1 个单位长度),用直尺和圆规画出下列向量.(1)|OA|=3,点 A 在点 O 正西方向;(2)|OB|=3,点 B 在点 O 北偏西 45°方向;(3)|OC|=2,点 C 在点 O 南偏东 60°方向.利用有向线段表示向量的基本步骤:(1)确定向量的起点;(2)确定向量的方向;(3)根据向量的模确定向量的终点.利用有向线段的起点和终点的字母表示向量时,必须是起点写在终点的前面.3.相等向量与共线向量活动与探究 3如图所示,△ABC 的三边均不相等,E,F,D 分别是 AC,AB,BC 的中点.(1)写出与EF共线的向量;(2)写出与EF的模大小相等的向量;(3)写出与EF相等的向量.迁移与应用如图所示,O 为正方形 ABCD 对角线的交点,四边形 OAED,四边形 OCFB 都是正方形.在图中所示的向量中:(1)分别写出与AO,BO相等的向量;(2)写出与AO共线的向量;(3)写出与AO的模相等的向量;(4)向量AO与CO是否相等?1.对共线向量与平行向量关系的认识(1)平行向量就是共线向量,这是因为任一组平行向量都可移到同一直线上(与有向线段的起点无关).(2)共线向量是指平行向量,与是否真的画在同一条直线上无关.2.在...