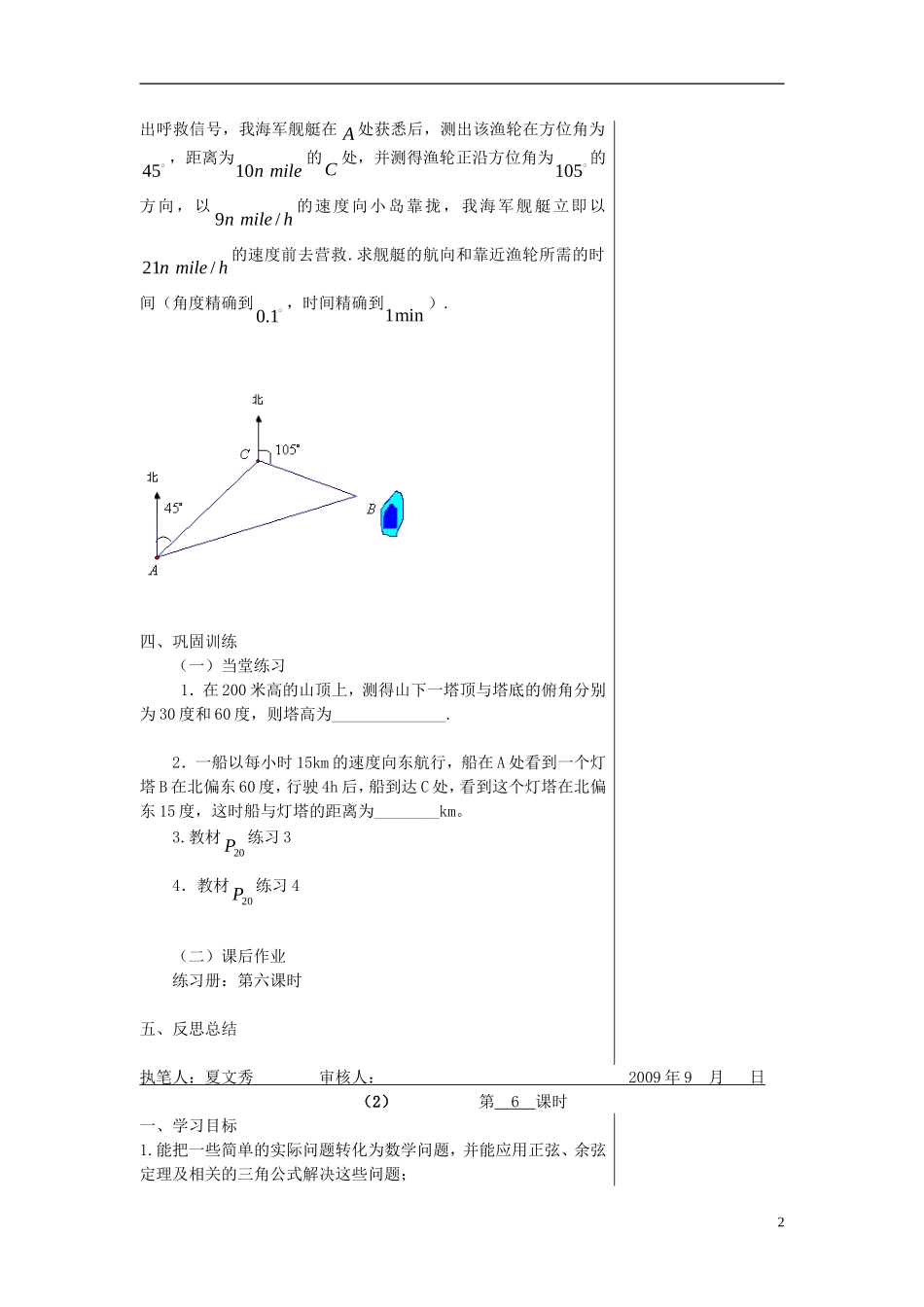
解三角形的实际应用举例一、学习目标 1.掌握用正弦定理,余弦定理解任意三角形的方法。2.会利用数学建模的思想,结合三角形的知识,解决生产实践中的相关问题二、学法指导1.了解常用的测量相关术语2.体会数学建模的基本思想,应用解三角形知识解决实际问题的解题一般步骤:①根据题意作出示意图;②确定所涉及的三角形,搞清已知和未知;③选用合适的定理进行求解;④给出答案。三、课前预习1.仰角和俯角在视线和水平线所成的角中,视线在水平线上方的角叫_____,在水平线下方的角叫_______.2.方位角指从正北方向顺时针转到目标方向线的角方位角的其他表示:(1)正南方向(2)东南方向(3)北偏东(4)南偏西 3.坡角:坡面与水平面的二面角的度数。三、课堂探究例 1 (教材18P 例 1)如图 1-3-1,为了测量河对岸两点,A B 之间 的 距 离 , 在 河 岸 这 边 取 点,C D , 测 得85ADC ,60BDC ,47ACD ,72BCD ,100CDm.设, ,,A B C D 在同一平面内,试求,A B 之间的距离(精确到1m ). 例 2 (教材18P 例 2)如图 1-3-2,某渔轮在航行中不幸遇险,发 1图1-3-11-3-1出呼救信号,我海军舰艇在 A 处获悉后,测出该渔轮在方位角为45 ,距离为10n mile的C 处,并测得渔轮正沿方位角为105 的方向,以 9/n mile h的速度向小岛靠拢,我海军舰艇立即以21/n mile h的速度前去营救.求舰艇的航向和靠近渔轮所需的时间(角度精确到0.1 ,时间精确到1min ).四、巩固训练(一)当堂练习 1.在 200 米高的山顶上,测得山下一塔顶与塔底的俯角分别为 30 度和 60 度,则塔高为______________.2.一船以每小时 15km 的速度向东航行,船在 A 处看到一个灯塔 B 在北偏东 60 度,行驶 4h 后,船到达 C 处,看到这个灯塔在北偏东 15 度,这时船与灯塔的距离为________km。3.教材20P 练习 34.教材20P 练习 4 (二)课后作业练习册:第六课时五、反思总结执笔人:夏文秀 审核人: 2009 年 9 月 日 (2) 第 6 课时一、学习目标 1.能把一些简单的实际问题转化为数学问题,并能应用正弦、余弦定理及相关的三角公式解决这些问题; 22.利用正弦定理、余弦定理等知识和方法解决一些几何和物理上的问题3.掌握利用数学建模解决实际问题的一般步骤。 二、学法指导能否灵活求解问题的关键是正弦定理和余弦定理的选用,有些题目只选用其一...