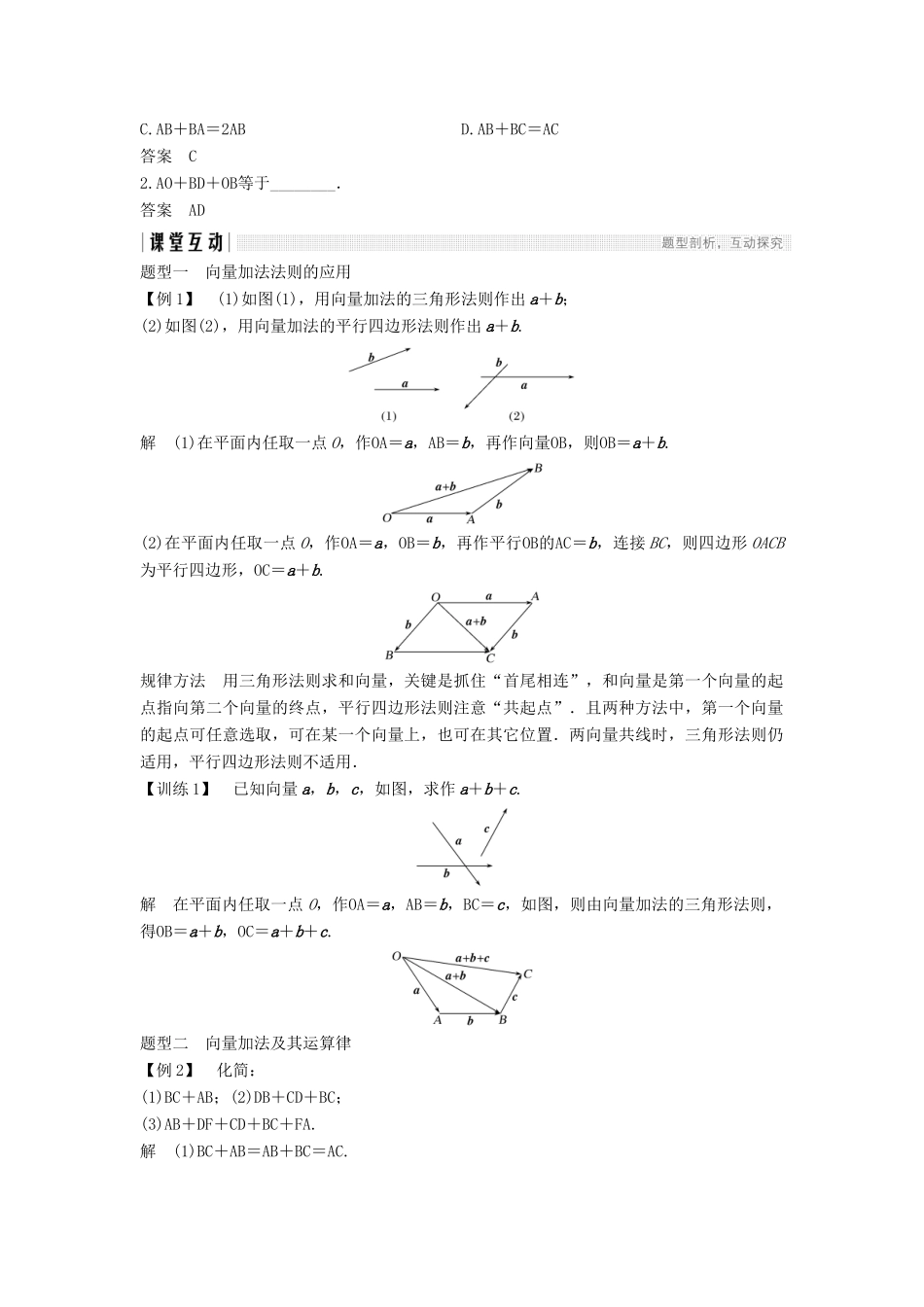
2.1 向量的加法内容要求 1.掌握向量加法的定义,会用向量加法的三角形法则和向量加法的平行四边形法则作两个向量的和向量(重点).2.掌握向量加法的交换律和结合律,并会用它们进行向量计算(难点).知识点 1 向量的加法(1)定义:求两个向量和的运算.(2)三角形法则:① 作图:已知向量 a,b,在平面上任取一点 A,作AB=a,BC=b,则向量AC叫作 a 与 b 的和,记作 a+b;② 几何意义:从第一个向量的起点到第二个向量终点的向量.(3)平行四边形法则:① 作图:已知向量 a,b,作AB=a,AD=b,以 AB,AD 为邻边作平行四边形 ABCD,则向量AC叫作 a 与 b 的和,表示为 a+b=AC;② 几何意义:平行四边形对角线所在的向量.【预习评价】1.在四边形 ABCD 中,AC=AB+AD,则( )A.ABCD 一定是矩形B.ABCD 一定是菱形C.ABCD 一定是正方形D.ABCD 一定是平行四边形答案 D2.在平行四边形 ABCD 中,BC+DC+BA=( )A.BC B.DA C.AB D.AC答案 A知识点 2 向量加法的运算律(1)交换律:a+b=b+a.(2)结合律:(a+b)+c=a+(b+c).特别地:对于零向量与任一向量 a 的和有 0+a=a+0=a.【预习评价】1.下列等式不成立的是( )A.0+a=aB.a+b=b+aC.AB+BA=2AB D.AB+BC=AC答案 C2.AO+BD+OB等于________.答案 AD题型一 向量加法法则的应用【例 1】 (1)如图(1),用向量加法的三角形法则作出 a+b;(2)如图(2),用向量加法的平行四边形法则作出 a+b.解 (1)在平面内任取一点 O,作OA=a,AB=b,再作向量OB,则OB=a+b.(2)在平面内任取一点 O,作OA=a,OB=b,再作平行OB的AC=b,连接 BC,则四边形 OACB为平行四边形,OC=a+b.规律方法 用三角形法则求和向量,关键是抓住“首尾相连”,和向量是第一个向量的起点指向第二个向量的终点,平行四边形法则注意“共起点”.且两种方法中,第一个向量的起点可任意选取,可在某一个向量上,也可在其它位置.两向量共线时,三角形法则仍适用,平行四边形法则不适用.【训练 1】 已知向量 a,b,c,如图,求作 a+b+c.解 在平面内任取一点 O,作OA=a,AB=b,BC=c,如图,则由向量加法的三角形法则,得OB=a+b,OC=a+b+c.题型二 向量加法及其运算律【例 2】 化简:(1)BC+AB;(2)DB+CD+BC;(3)AB+DF+CD+BC+FA.解 (1)BC+AB=AB+BC=AC.(2)DB+CD+BC=BC+CD+DB=(BC+CD)+DB=BD+DB=0.(3)AB+DF+CD+BC+FA=AB...