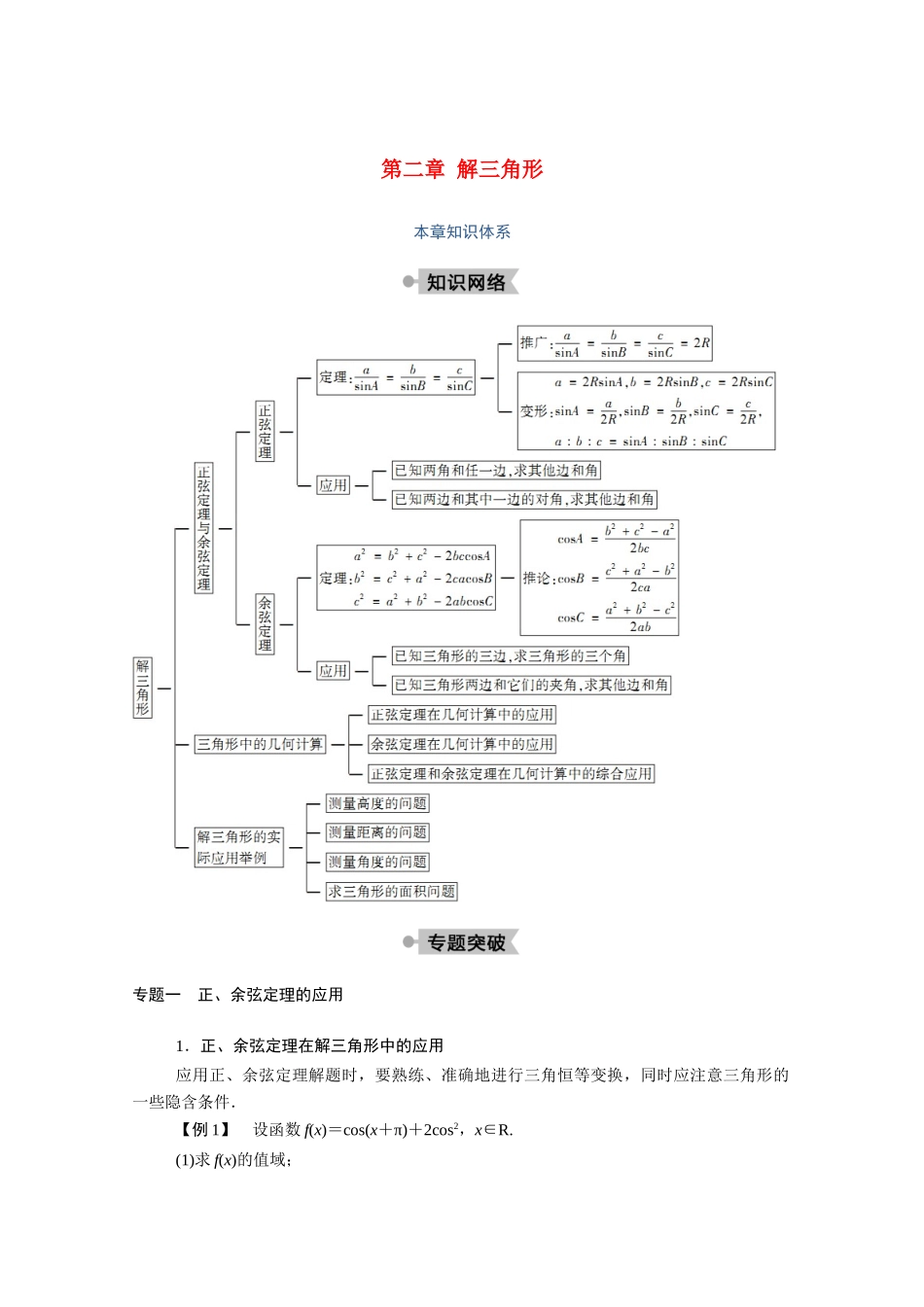
第二章 解三角形本章知识体系专题一 正、余弦定理的应用 1.正、余弦定理在解三角形中的应用应用正、余弦定理解题时,要熟练、准确地进行三角恒等变换,同时应注意三角形的一些隐含条件.【例 1】 设函数 f(x)=cos(x+π)+2cos2,x∈R.(1)求 f(x)的值域;(2)记△ABC 的内角 A、B、C 的对边长分别为 a、b、c,若 f(B)=1,b=1,c=,求 a 的值.【思路探究】 本题考查了三角函数的化简求值及解斜三角形的有关知识.对于 (1)先把 f(x)化简为 Asin(ωx+φ)的形式,再进行求值,(2)问可先求出 B 的值再利用余弦定理解决.【解答】 (1)f(x)=cosxcosπ-sinxsinπ+cosx+1=-cosx-sinx+cosx+1=cosx-sinx+1=sin(x+)+1.因此 f(x)的值域为[0,2].(2)由 f(B)=1 得 sin(B+)+1=1,即 sin(B+)=0,又因 0