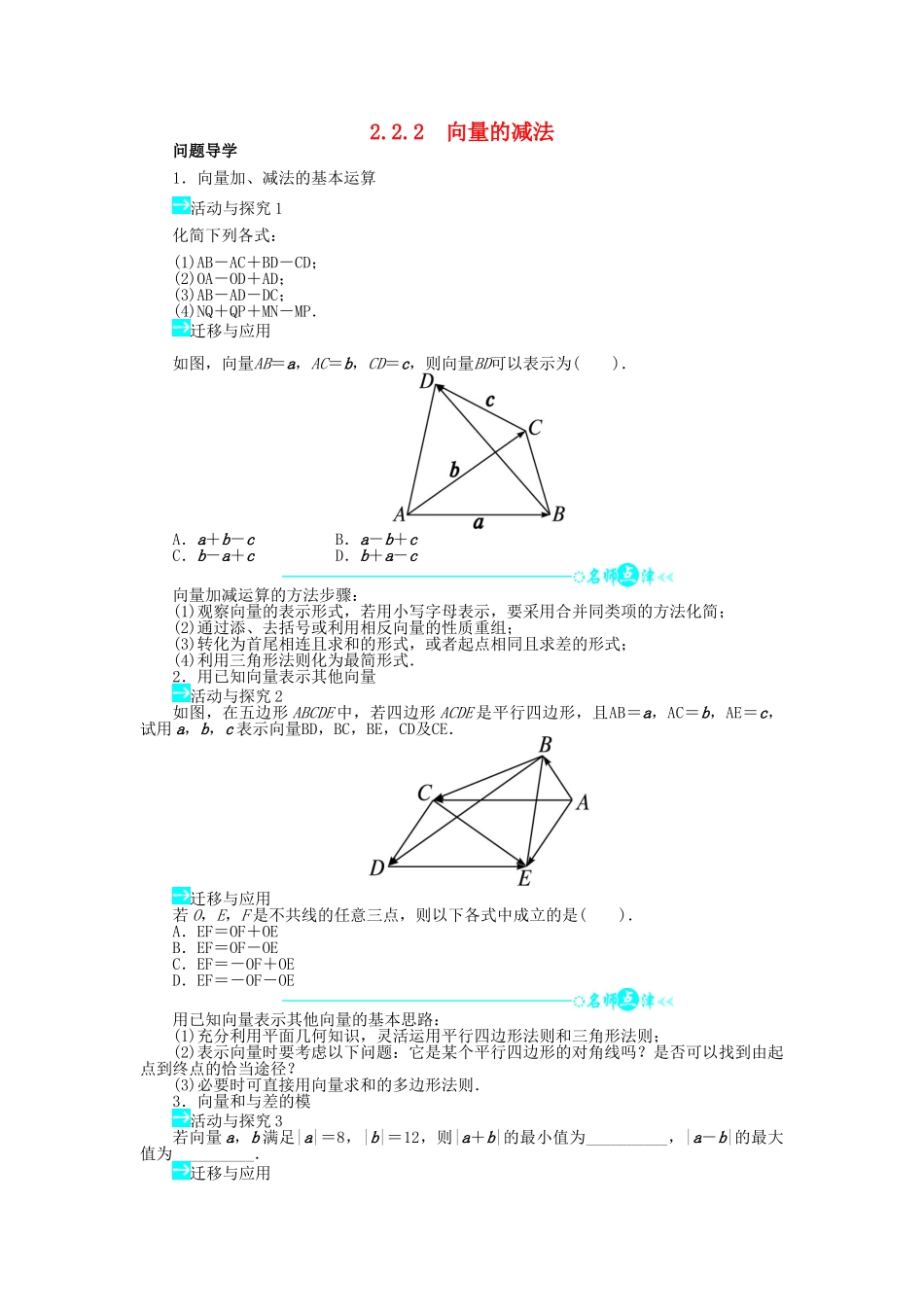
2.2.2 向量的减法问题导学1.向量加、减法的基本运算活动与探究 1化简下列各式:(1)AB-AC+BD-CD;(2)OA-OD+AD;(3)AB-AD-DC;(4)NQ+QP+MN-MP.迁移与应用如图,向量AB=a,AC=b,CD=c,则向量BD可以表示为( ).A.a+b-c B.a-b+cC.b-a+c D.b+a-c向量加减运算的方法步骤:(1)观察向量的表示形式,若用小写字母表示,要采用合并同类项的方法化简;(2)通过添、去括号或利用相反向量的性质重组;(3)转化为首尾相连且求和的形式,或者起点相同且求差的形式;(4)利用三角形法则化为最简形式.2.用已知向量表示其他向量活动与探究 2如图,在五边形 ABCDE 中,若四边形 ACDE 是平行四边形,且AB=a,AC=b,AE=c,试用 a,b,c 表示向量BD,BC,BE,CD及CE.迁移与应用若 O,E,F 是不共线的任意三点,则以下各式中成立的是( ).A.EF=OF+OEB.EF=OF-OEC.EF=-OF+OED.EF=-OF-OE用已知向量表示其他向量的基本思路:(1)充分利用平面几何知识,灵活运用平行四边形法则和三角形法则;(2)表示向量时要考虑以下问题:它是某个平行四边形的对角线吗?是否可以找到由起点到终点的恰当途径?(3)必要时可直接用向量求和的多边形法则.3.向量和与差的模活动与探究 3若向量 a,b 满足|a|=8,|b|=12,则|a+b|的最小值为__________,|a-b|的最大值为__________.迁移与应用1.已知向量 a,b 满足|a|=3,|a+b|=|a-b|=5,则|b|=________.2.在△ABC 中,∠C=90°,|AC|=5,|BC|=12,设 a=CA,b=CB,则 a-b 的大小是________,a-b 的方向是________.两个向量的和与差的模满足||a|-|b||≤|a±b|≤|a|+|b|,只有当 a 与 b 共线时,等号才有可能成立.在这里,应注意:|a|-|b|与|a-b|的最小值是不一样的,前者可能为负,而后者一定非负.当堂检测1.在△ABC 中,D,E,F 分别为 AB,BC,CA 的中点,则AF-DB等于( ).A.FD B.FC C.FE D.BE2.下列等式中正确的个数是( ).①a-0=a;② b+a=a+b;③-(-a)=a;④ a+(-a)=0;⑤ a+(-b)=a-b.A.2 B.3 C.4 D.53.若向量 a 与 b 反向,且|a|=|b|=1,则|a-b|等于( ).A.0 B.1 C. D.24.AB+BC-AC=__________.5.如图所示,已知一点 O 到平行四边形 ABCD 的三个顶点 A、B、C 的向量分别为r1,r2,r3,求OD. 提示:用最精炼的语言把你当堂掌握的核心知识的精华部分和基本技能的...