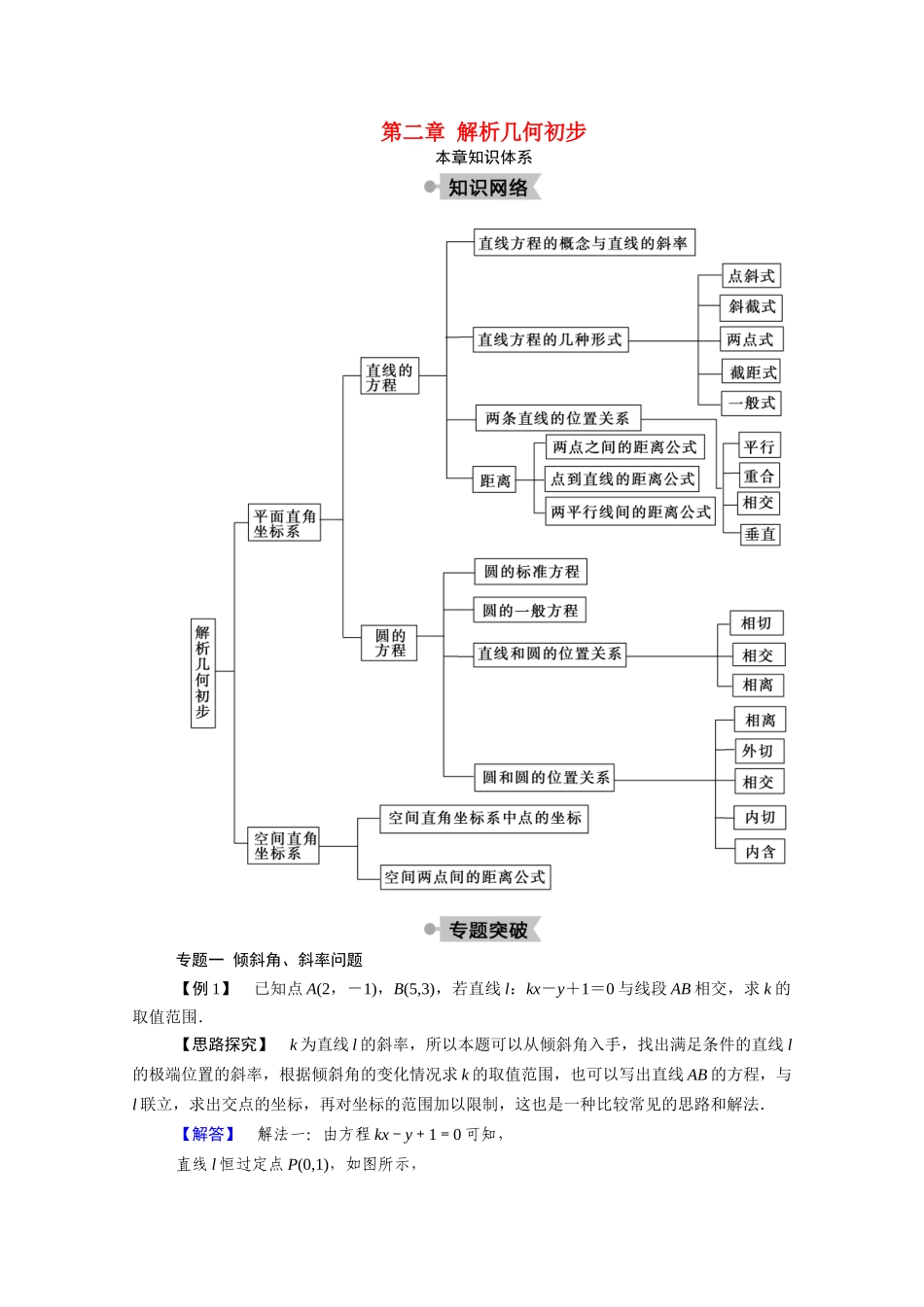
第二章 解析几何初步本章知识体系专题一 倾斜角、斜率问题 【例 1】 已知点 A(2,-1),B(5,3),若直线 l:kx-y+1=0 与线段 AB 相交,求 k 的取值范围.【思路探究】 k 为直线 l 的斜率,所以本题可以从倾斜角入手,找出满足条件的直线 l的极端位置的斜率,根据倾斜角的变化情况求 k 的取值范围,也可以写出直线 AB 的方程,与l 联立,求出交点的坐标,再对坐标的范围加以限制,这也是一种比较常见的思路和解法.【解答】 解法一:由方程 kx-y+1=0 可知,直线 l 恒过定点 P(0,1),如图所示,连接 PA,PB,解得 kPA=-1,kPB=.又 直线 l 的斜率为 k,∴k 的取值范围为-1≤k≤.解法二:由两点式求得直线 AB 的方程为 4x-3y-11=0,联立方程组解得 x=-,满足 2≤≤5,解得-1≤k≤.已知实数 x,y 满足 y=-2x+8,且 2≤x≤3,求的最大值和最小值.解:如图,由已知,点 P(x,y)在线段 AB 上运动,其中 A(2,4),B(3,2),而=,其几何意义为直线 OP 的斜率,由图可知 kOB≤kOP≤kOA,而 kOB=,kOA=2.故所求的的最大值为 2,最小值为.专题二 直线的方程 【例 2】 设直线 l 的方程为(m+1)x+y+2-m=0(m∈R).(1)若 l 在两坐标轴上的截距相等,求直线 l 的方程;(2)若直线 l 不经过第二象限,求实数 m 的取值范围.【解答】 (1)当直线过原点时,该直线在 x 轴和 y 轴上的截距为零,显然相等,所以 m=2 满足条件,此时直线 l 的方程为 3x+y=0.当 m=-1 时,直线为平行于 x 轴的直线,在 x 轴上无截距,不合题意.当 m≠-1 且 m≠2 时,直线在 x 轴上的截距为,直线在 y 轴上的截距为 m-2,因此=m-2,即 m+1=1,所以 m=0,此时直线 l 的方程为 x+y+2=0.综上所述,当 m=2 或 m=0 时,直线 l 在两坐标轴上的截距相等,方程为 3x+y=0 或x+y+2=0.(2)将 l 的方程转化为 y=-(m+1)x+m-2,所以或所以 m≤-1,所以 m 的取值范围为(-∞,-1].已知直线的斜率为,且和坐标轴围成面积为 3 的三角形,求该直线方程.解:设直线方程为 y=x+b,则该直线在两坐标轴上的截距分别为 b,-6b,∴S=|b|·|-6b|=3b2=3,∴b=±1,∴直线方程为 x-6y+6=0 或 x-6y-6=0.专题三 两直线位置关系 【例 3】 已知两条直线 l1:ax+3y-3=0,l2:4x+6y-1=0,若 l1∥l2,则 a=________....