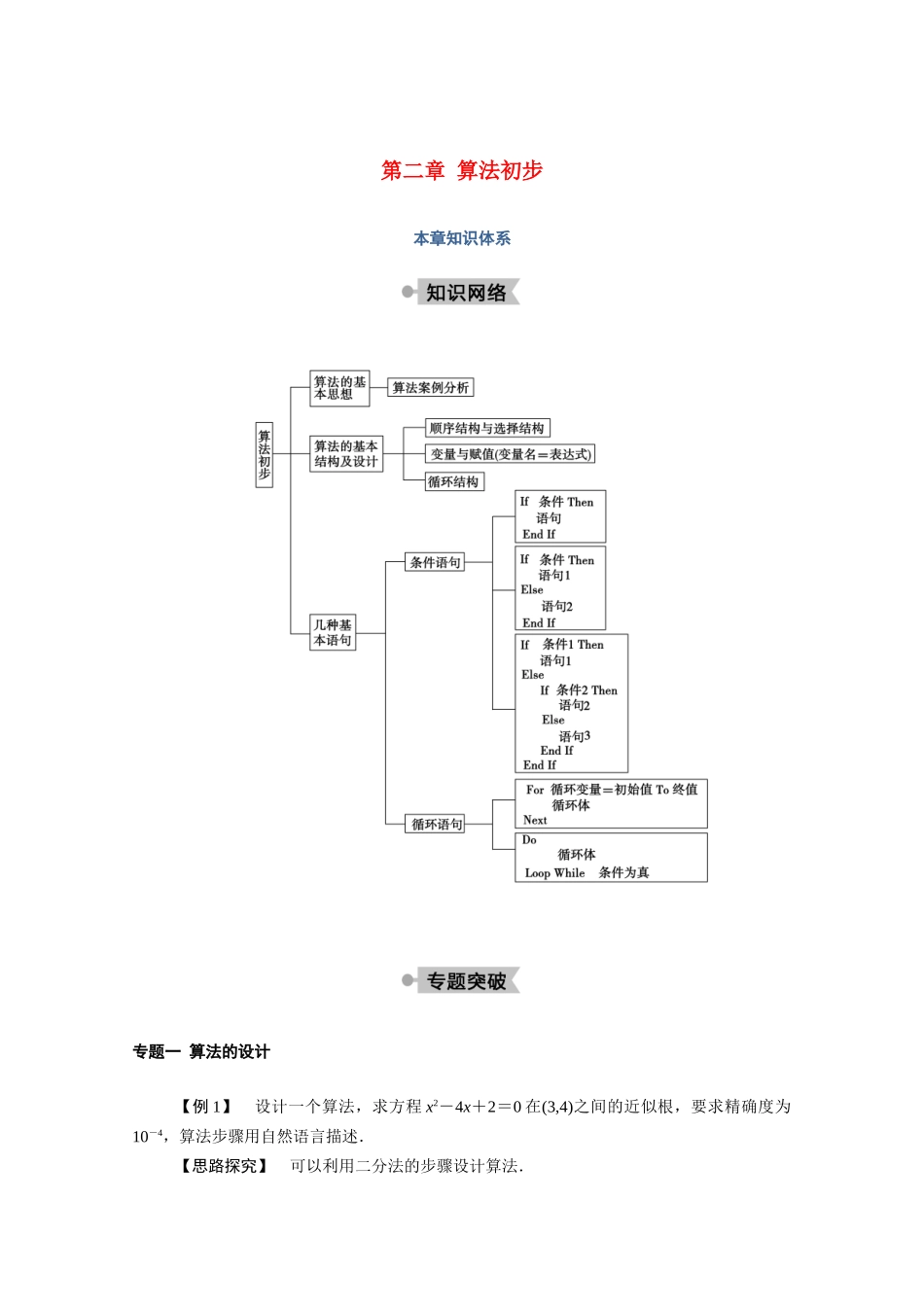
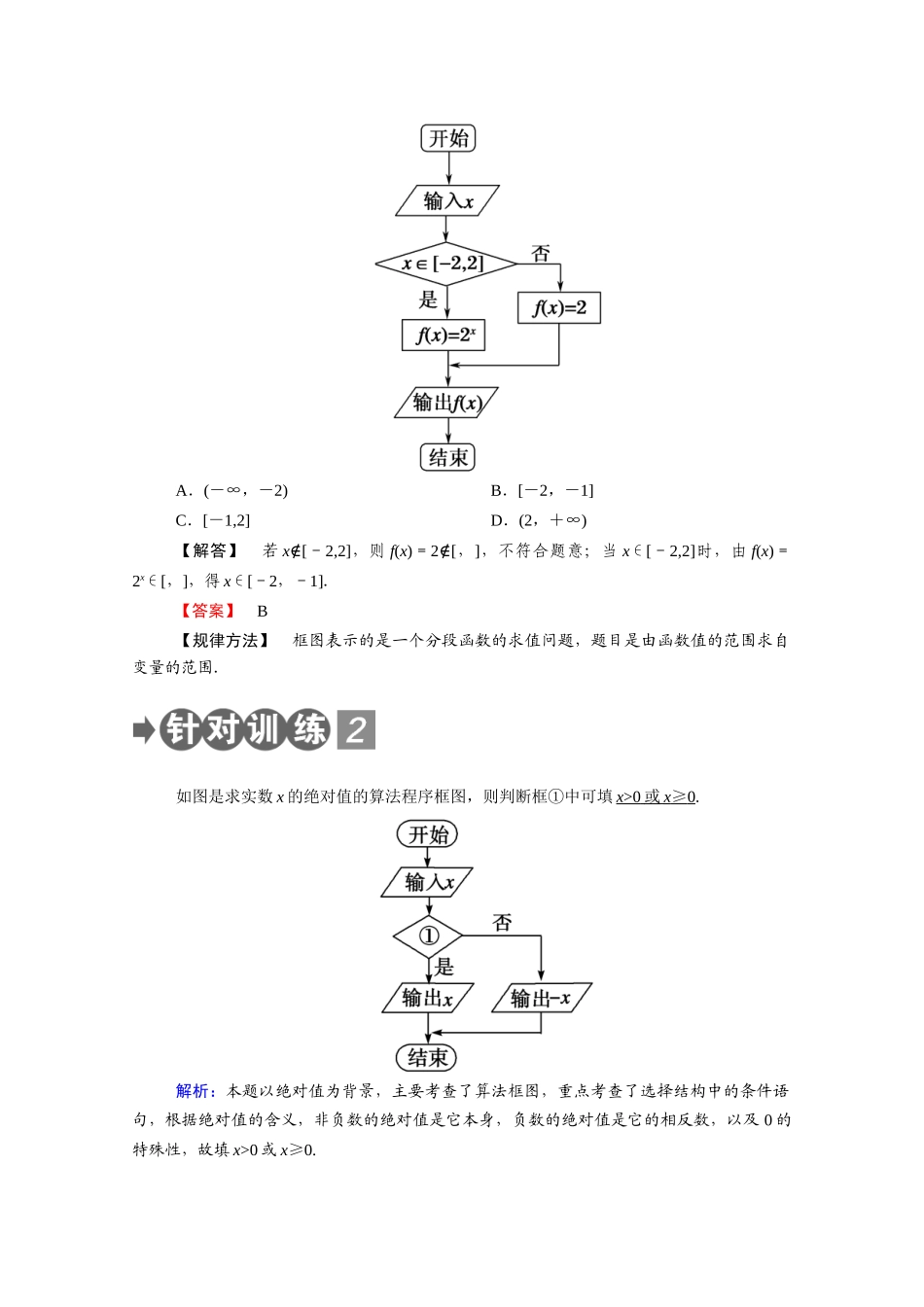
第二章 算法初步本章知识体系 专题一 算法的设计 【例 1】 设计一个算法,求方程 x2-4x+2=0 在(3,4)之间的近似根,要求精确度为10-4,算法步骤用自然语言描述.【思路探究】 可以利用二分法的步骤设计算法.【解答】 算法步骤如下:第一步,令 f(x)=x2-4x+2,由于 f(3)=-1<0,f(4)=2>0,所以设 x1=3,x2=4.第二步,令 m=,判断 f(m)是否等于 0,若 f(m)=0,则 m 为所求的根,结束算法;若f(m)≠0,则执行第三步.第三步,判断 f(x1)f(m)>0 是否成立,若成立,则令 x1=m;否则令 x2=m.第四步,判断|x1-x2|<10-4是否成立,若成立,则 x1与 x2之间的任意取值均为满足条件的近似根;若不成立,则返回第二步.【规律方法】 (1)算法设计与一般意义上的解决问题不同,它是对一类问题的一般解法的抽象与概括,它往往是把问题的解法划分为若干个可执行的步骤,有时是重复多次,但最终都必须在有限个步骤之内完成.(2)对于给定的问题,设计其算法时应注意以下四点:① 与解决问题的一般方法相联系,从中提炼与概括步骤;② 将解决问题的过程划分为若干步骤;③ 引入有关的参数或变量对算法步骤加以表述;④ 用简练的语言将各个步骤表达出来.已知平面坐标系中两点 A(-1,0),B(3,2),写出求线段 AB 的垂直平分线方程的一个算法.解:第一步,计算 x0===1,y0==1,得 AB 的中点 N(1,1).第二步,计算 k1==,得 AB 的斜率.第三步,计算 k=-=-2,得 AB 垂直平分线的斜率.第四步,由点斜式得直线 AB 的垂直平分线的方程:y-1=-2(x-1),即 2x+y-3=0.专题二 算法的选择结构 【例 2】 阅读如图所示的算法框图,如果输出的函数值在区间[,]内,则输入的实数x 的取值范围是( )A.(-∞,-2) B.[-2,-1]C.[-1,2] D.(2,+∞)【解答】 若 x∉[-2,2],则 f(x)=2∉[,],不符合题意;当 x∈[-2,2]时,由 f(x)=2x∈[,],得 x∈[-2,-1].【答案】 B【规律方法】 框图表示的是一个分段函数的求值问题,题目是由函数值的范围求自变量的范围.如图是求实数 x 的绝对值的算法程序框图,则判断框①中可填 x >0 或 x ≥ 0 .解析:本题以绝对值为背景,主要考查了算法框图,重点考查了选择结构中的条件语句,根据绝对值的含义,非负数的绝对值是它本身,负数的绝对值是它的相反数,以及 0 的特殊性,故填 x>0 或 x≥0.专题三 算法的循环结构 ...