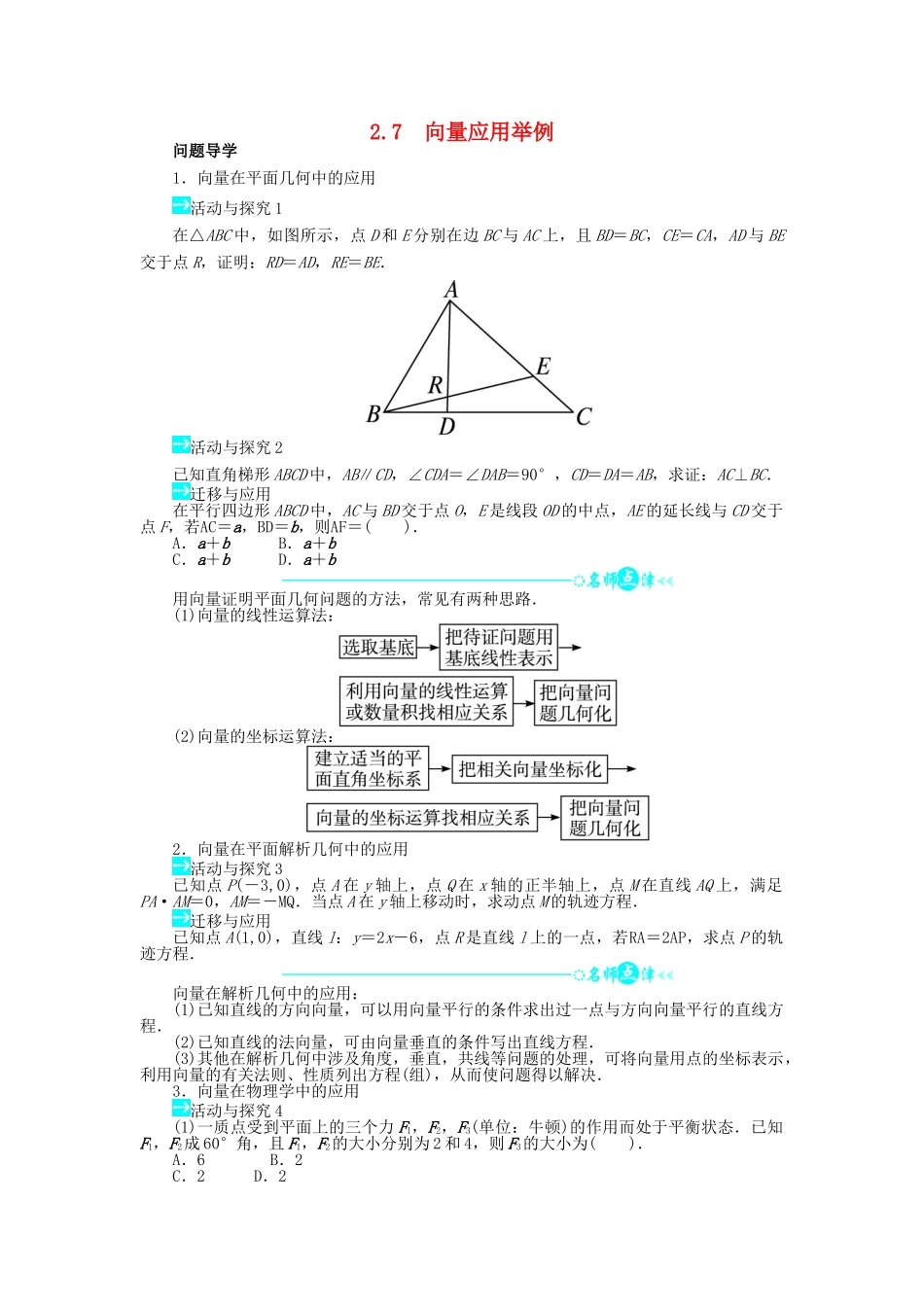
2.7 向量应用举例问题导学1.向量在平面几何中的应用活动与探究 1在△ABC 中,如图所示,点 D 和 E 分别在边 BC 与 AC 上,且 BD=BC,CE=CA,AD 与 BE交于点 R,证明:RD=AD,RE=BE.活动与探究 2已知直角梯形 ABCD 中,AB∥CD,∠CDA=∠DAB=90°,CD=DA=AB,求证:AC⊥BC.迁移与应用在平行四边形 ABCD 中,AC 与 BD 交于点 O,E 是线段 OD 的中点,AE 的延长线与 CD 交于点 F,若AC=a,BD=b,则AF=( ).A.a+b B.a+bC.a+b D.a+b用向量证明平面几何问题的方法,常见有两种思路.(1)向量的线性运算法:(2)向量的坐标运算法:2.向量在平面解析几何中的应用活动与探究 3已知点 P(-3,0),点 A 在 y 轴上,点 Q 在 x 轴的正半轴上,点 M 在直线 AQ 上,满足PA·AM=0,AM=-MQ.当点 A 在 y 轴上移动时,求动点 M 的轨迹方程.迁移与应用已知点 A(1,0),直线 l:y=2x-6,点 R 是直线 l 上的一点,若RA=2AP,求点 P 的轨迹方程.向量在解析几何中的应用:(1)已知直线的方向向量,可以用向量平行的条件求出过一点与方向向量平行的直线方程.(2)已知直线的法向量,可由向量垂直的条件写出直线方程.(3)其他在解析几何中涉及角度,垂直,共线等问题的处理,可将向量用点的坐标表示,利用向量的有关法则、性质列出方程(组),从而使问题得以解决.3.向量在物理学中的应用活动与探究 4(1)一质点受到平面上的三个力 F1,F2,F3(单位:牛顿)的作用而处于平衡状态.已知F1,F2成 60°角,且 F1,F2的大小分别为 2 和 4,则 F3的大小为( ).A.6 B.2C.2 D.2(2)一辆汽车在平直公路上向西行驶,车上装着风速计和风向标,测得风向为东偏南30°,风速为 4 米/秒,这时气象台报告实际风速为 2 米/秒.试求风的实际方向和汽车的速度大小.迁移与应用如图,无弹性的细绳 OA,OB 的一端分别固定在 A,B 处,同质量的细绳 OC 下端系着一个秤盘,且使得 OB⊥OC,试分析 OA,OB,OC 哪根绳受力最大?用力向量和速度向量解决物理问题的方法步骤:(1)把物理问题中的相关量用向量表示;(2)转化为向量问题的模型,通过向量运算使问题得以解决;(3)还原为物理问题.注意:力、速度、加速度、位移都是向量;其中功 W=F·s 即功是力 F 与所产生位移 s的数量积;动量 mv 是数乘向量等.当堂检测1.若向量OF1=(1,1),OF2=(-3,-2)分别表示两个力 F1...