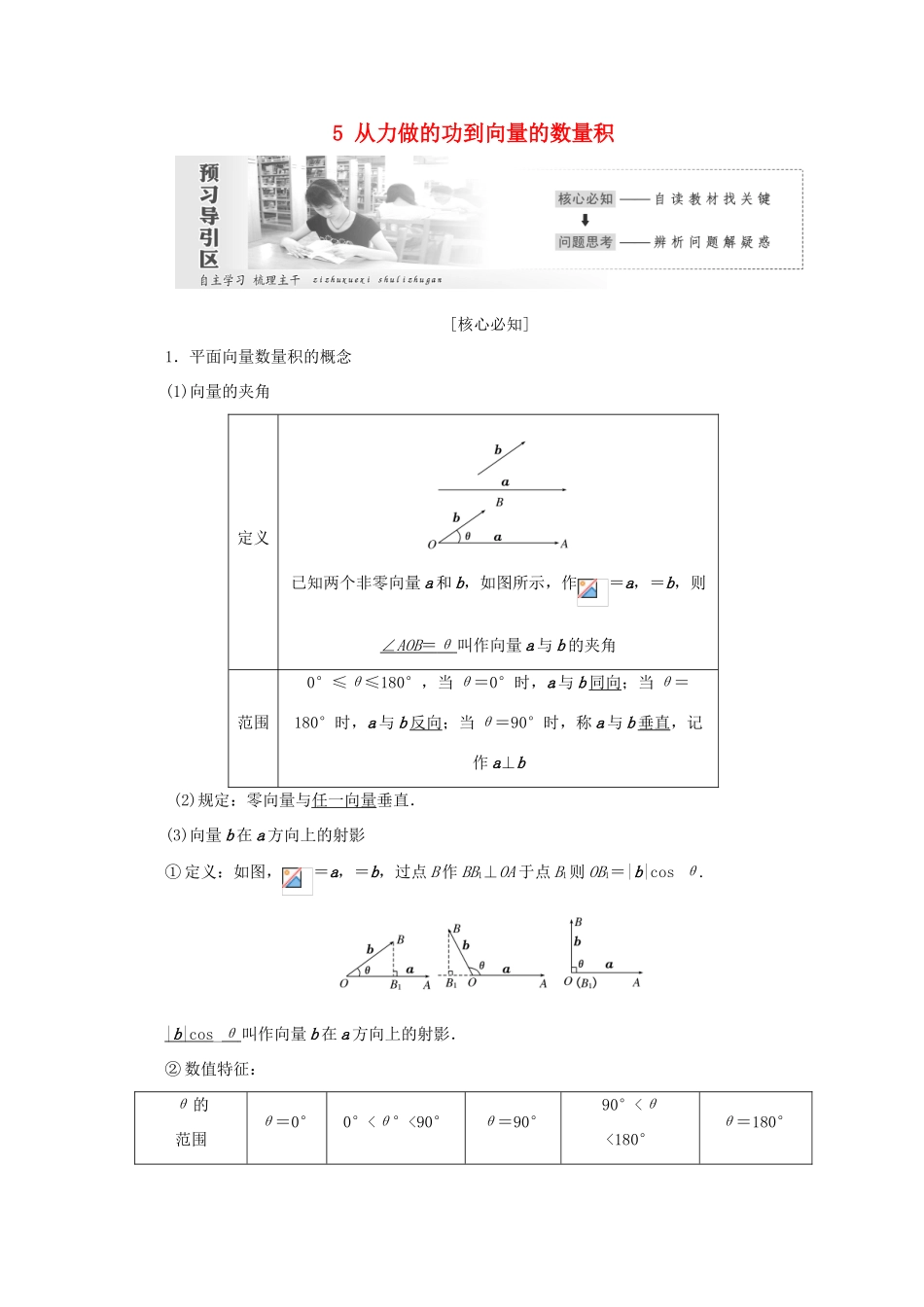
5 从力做的功到向量的数量积[核心必知]1.平面向量数量积的概念(1)向量的夹角定义已知两个非零向量 a 和 b,如图所示,作=a,=b,则∠ AOB = θ 叫作向量 a 与 b 的夹角范围0°≤θ≤180°,当 θ=0°时,a 与 b 同向;当 θ=180°时,a 与 b 反向;当 θ=90°时,称 a 与 b 垂直,记作 a⊥b (2)规定:零向量与任一向量垂直.(3)向量 b 在 a 方向上的射影① 定义:如图,=a,=b,过点 B 作 BB1⊥OA 于点 B1则 OB1=|b|cos θ.| b | cos _θ 叫作向量 b 在 a 方向上的射影.② 数值特征:θ 的范围θ=0°0°<θ°<90°θ=90°90°<θ<180°θ=180°续表图形正负正数|b|正数0负数负数-|b|(4)向量的数量积定义已知两个向量 a 和 b,它们的夹角为 θ,把|a||b|cos θ 叫作 a 与 b 的数量积(或内积),记作 a·b,即 a·b=|a||b|cos θ几何意义a 与 b 的数量积等于 a 的长度|a|与 b 在 a 方向上射影|b|cos θ 的乘积,或 b 的长度|b|与 a 在 b 方向上射影|a|cos θ 的乘积物理意义力对物体做功,就是力 F 与其作用下物体的位移 s 的数量积 F · s 2.数量积的性质(1)若 e 是单位向量,则 e·a=a·e=| a | cos _θ.(2)若 a⊥b,则 a·b=0;反之,若 a·b=0,则 a⊥b.通常记作 a ⊥ b ⇔ a · b = 0 .(3)|a|=.(4)cos θ=(|a||b|≠0)(5)对任意两个向量 a,b,有|a·b|≤|a||b|.当且仅当 a ∥ b 时等号成立.3.数量积的运算律若给定向量 a,b,c 和实数 λ,则数量积满足:(1)交换律:a·b=b · a ;(2)数乘向量结合律:(λa)·b=λ ( a · b ) =a ·( λ b ) ;(3)分配律:a·(b+c)=a · b + a · c .[问题思考]1.向量 b 在 a 方向上的射影仍是一个向量,对吗?提示:不对.向量 b 在 a 方向上的射影不是向量而是数量,它的符号取决于两向量夹角 θ的取值范围.2.两向量 a 与 b 的数量积是一个向量,对吗?提示:不对.向量的数量积是一个实数,其值可正,可负,可以为 0.讲一讲1.已知向量 a 与 b 的夹角 θ=120°,且|a|=4,|b|=2,求(1)a·(-b);(2)(a-2b)·(a+b)[尝试解答] (1) 向量 a 与 b 的夹角 θ=120°,∴向量 a 与-b 的夹角为 180°-θ=60°.∴a·(-b)=|a|·|b|·cos 60°=4·2·=4.(2)(a-2b)·(a+b)=a2+a...