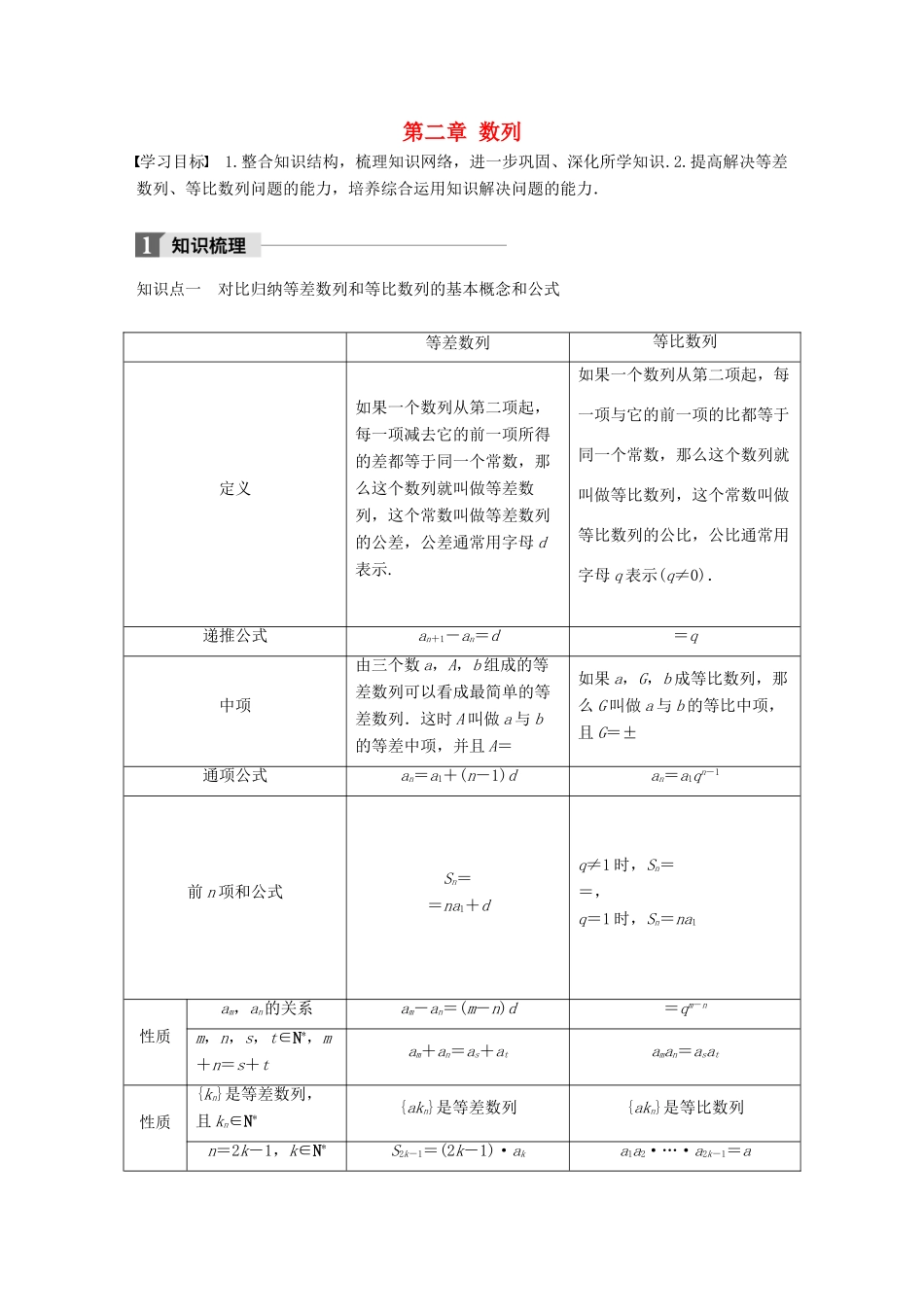
第二章 数列学习目标 1.整合知识结构,梳理知识网络,进一步巩固、深化所学知识.2.提高解决等差数列、等比数列问题的能力,培养综合运用知识解决问题的能力.知识点一 对比归纳等差数列和等比数列的基本概念和公式等差数列等比数列定义如果一个数列从第二项起,每一项减去它的前一项所得的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母 d表示.如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母 q 表示(q≠0).递推公式an+1-an=d=q中项由三个数 a,A,b 组成的等差数列可以看成最简单的等差数列.这时 A 叫做 a 与 b的等差中项,并且 A=如果 a,G,b 成等比数列,那么 G 叫做 a 与 b 的等比中项,且 G=±通项公式an=a1+(n-1)dan=a1qn-1前 n 项和公式Sn==na1+dq≠1 时,Sn==,q=1 时,Sn=na1性质am,an的关系am-an=(m-n)d=qm-nm,n,s,t∈N*,m+n=s+tam+an=as+ataman=asat性质{kn}是等差数列,且 kn∈N*{akn}是等差数列{akn}是等比数列n=2k-1,k∈N*S2k-1=(2k-1)·aka1a2·…·a2k-1=a判断方法利用定义an+1-an是同一个常数是同一个常数利用中项an+an+2=2an+1anan+2=a利用通项公式an=pn+q,其中 p、q 为常数an=abn(a≠0,b≠0)利用前 n 项和公式Sn=an2+bn (a,b 为常数)Sn=A(qn-1),其中A≠0,q≠0 且 q≠1 或 Sn=np(p 为非零常数)知识点二 数列中的公式推导和解题过程中用到的基本方法和思想1.在求等差数列和等比数列的通项公式时,分别用到了________法和________法.2.在求等差数列和等比数列的前 n 项和时,分别用到了________________法和________________法.3.等差数列和等比数列各自都涉及 5 个量,已知其中任意________个求其余________个,用到了方程思想.4.在研究等差数列和等比数列单调性,等差数列前 n 项和最值问题时,都用到了________________思想.类型一 方程思想求解数列问题例 1 设{an}是公比大于 1 的等比数列,Sn 为数列{an}的前 n 项和.已知 S3=7,且 a1+3,3a2,a3+4 构成等差数列公式.(1)求数列{an}的通项公式; (2)令 bn=ln a3n+1,n=1,2,…,求数列{bn}的前 n 项和 Tn. 反思与感悟 在等差数列和等比数列中,通项公式 an 和前 n 项和...