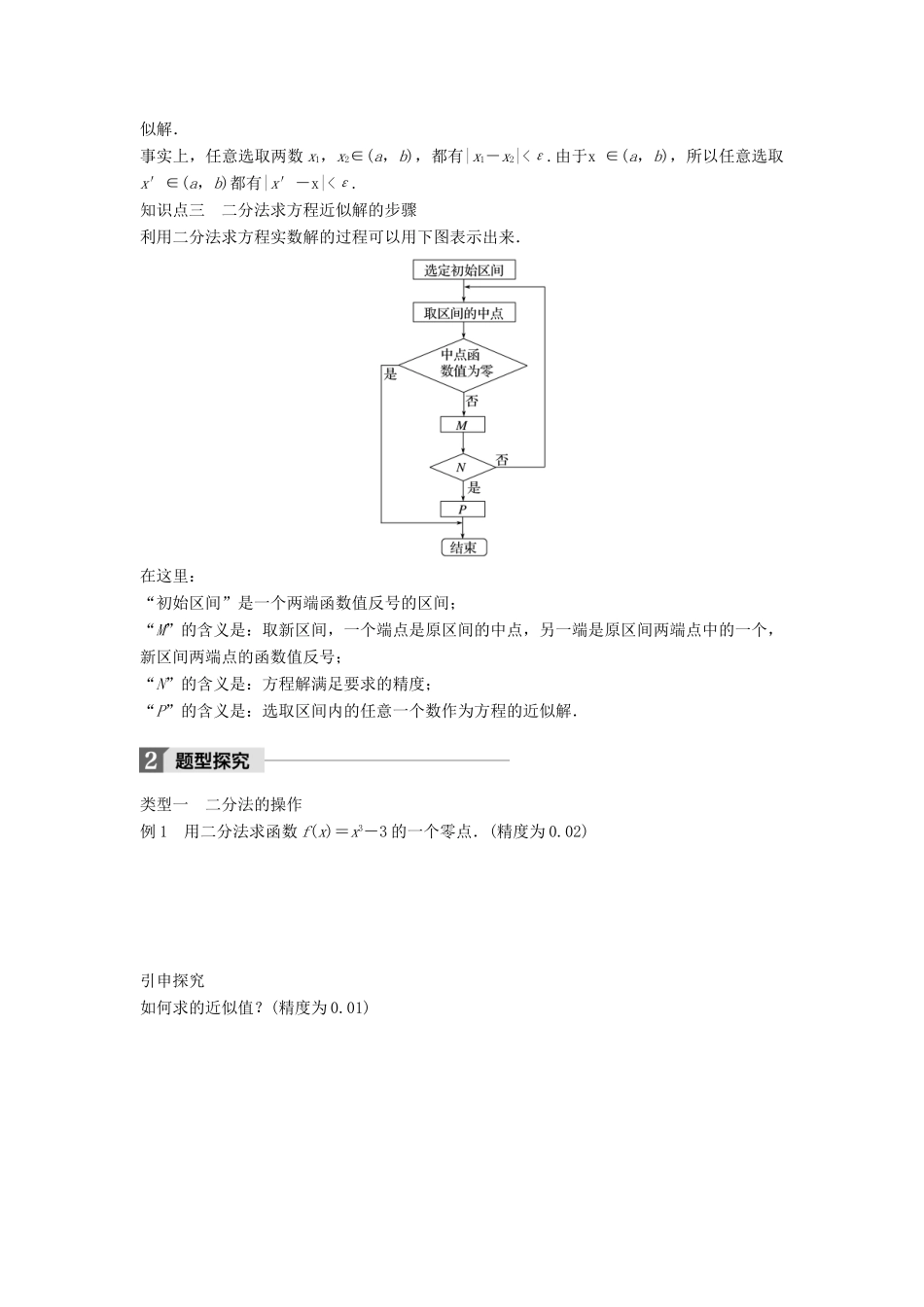
1.2 利用二分法求方程的近似解学习目标 1.理解二分法的原理及其适用条件.2.掌握二分法的实施步骤.3.体会二分法中蕴含的逐步逼近与程序化思想.知识点一 二分法的原理思考 通过上节课的学习,我们知道 f(x)=ln x+2x-6 的零点在区间(2,3)内,如何缩小零点所在区间(2,3)的范围? 梳理 二分法的概念如果在区间[a,b]上,函数 f(x)的图像是______________________,且__________________,则区间[a,b]内有方程 f(x)=0 的解.依次取有解________________,如果取到某个区间的中点 x0,恰使 f(x0)=0,则 x0就是所求的一个解;如果区间中点的函数值总不等于零,那么,不断地重复上述操作,就得到一系列闭区间,方程的一个解在这些区间中,区间长度____________,端点逐步逼近方程的解,可以得到一个近似解.像这样每次__________________,________________________,再经比较,按需要留下其中一个小区间的方法称为二分法.知识点二 精度与精确到思考 “精确到 0.1”与“精度为 0.1”一样吗? 梳理 在许多实际应用中,不需要求出方程精确的解,只要满足一定的精度就可以.设 x 是方程 f(x)=0 的一个解,给定正数 ε,若 x0满足__________________,就称 x0是满足精度 ε 的近似解.为 了 得 到 满 足 精 度 ε 的 近 似 解 , 只 需 找 到 方 程 的 一 个 有 解 区 间[a,b],________________________,那么区间(a,b)内任意一个数都是满足精度 ε 的近似解.事实上,任意选取两数 x1,x2∈(a,b),都有|x1-x2|<ε.由于x ∈(a,b),所以任意选取x′∈(a,b)都有|x′-x|<ε.知识点三 二分法求方程近似解的步骤利用二分法求方程实数解的过程可以用下图表示出来.在这里:“初始区间”是一个两端函数值反号的区间;“M”的含义是:取新区间,一个端点是原区间的中点,另一端是原区间两端点中的一个,新区间两端点的函数值反号;“N”的含义是:方程解满足要求的精度;“P”的含义是:选取区间内的任意一个数作为方程的近似解.类型一 二分法的操作例 1 用二分法求函数 f(x)=x3-3 的一个零点.(精度为 0.02)引申探究如何求的近似值?(精度为 0.01) 反思与感悟 用二分法求函数零点的近似值关键有两点:一是初始区间的选取,符合条件(包括零点),又要使其长度尽量小;二是进行精度的判断,以决定是停止计算还是继续计算.跟踪训练 1 借助计算器或计算机用二分法求方程 2x...