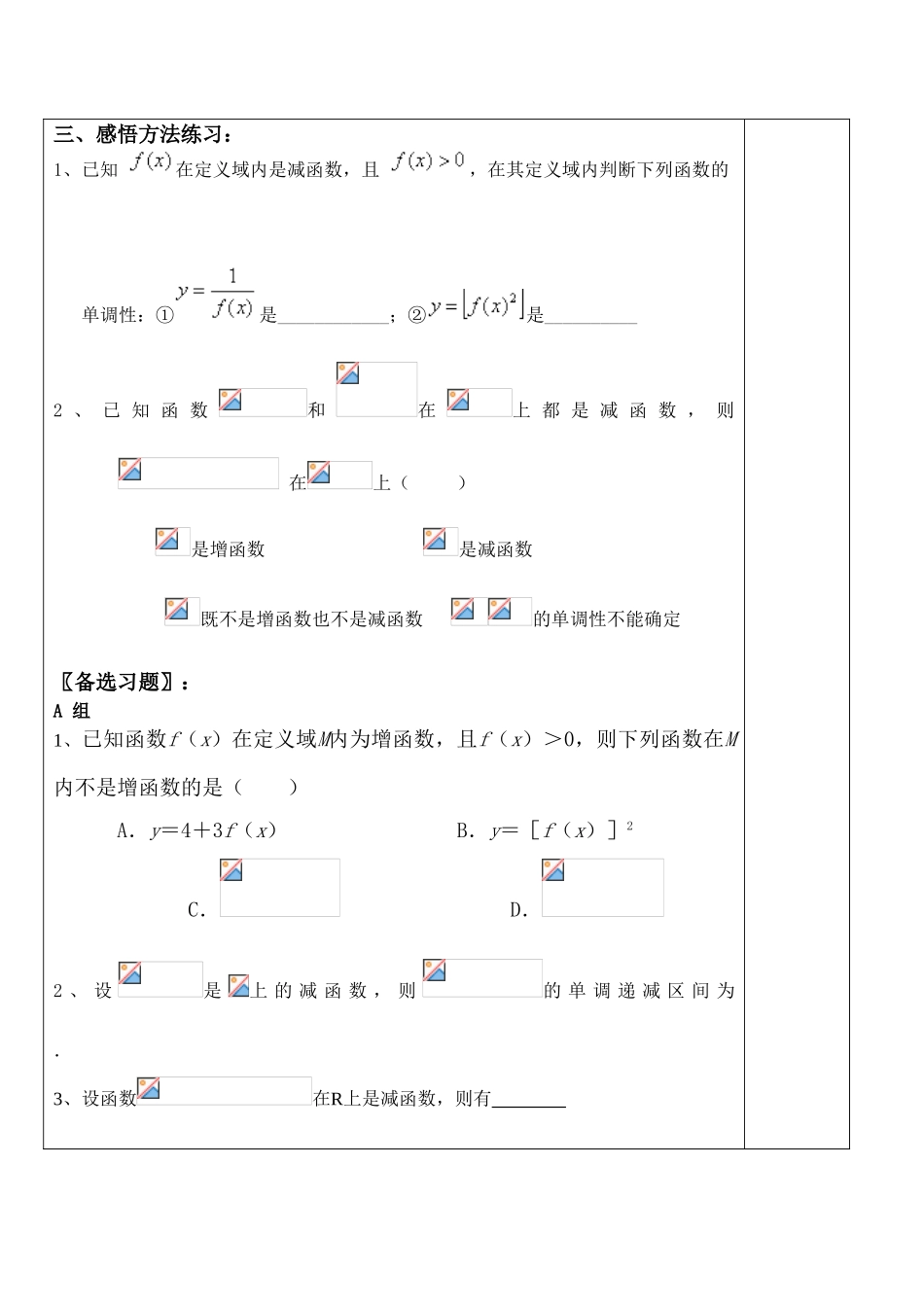
函数的单调性 讲学案(二)〖学习目标及要求〗:1、学习目标:(1)进一步掌握单调性,会求复合函数的单调区间;(2)会应用单调性解题;(3)培养学生发现问题、分析问题、解决问题的能力. 2、重点难点:复合函数的单调区间3、高考要求:理解函数单调性。4、体现的思想方法:探索发现、数形结合、归纳转化。5、知识体系的建构:特殊一般。〖讲学过程〗: 一、预习反馈: 二、探究精讲:探究一:1. 函数 , ,求函数 的单调区间.2、如果函数f(x)=(a2-1)x在R上是减函数,那么实数a的取值范围是( ) A.|a|>1B.|a|<2 C.|a|>3D.1<|a|<探究二: “菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点(大约是在距地面高度25 m到30 m处)时爆裂.如果在距地面高度18 m的地方点火,并且烟花冲出的速度是14.7 m/s.(1)写出烟花距地面的高度与时间之间的关系式.(2)烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少?(精确到1 m)感悟归纳一: 感悟归纳二: 三、感悟方法练习:1、已知 在定义域内是减函数,且 ,在其定义域内判断下列函数的单调性:①是____________;②是__________ 2 、 已 知 函 数和在上 都 是 减 函 数 , 则 在上( )是增函数 是减函数既不是增函数也不是减函数 的单调性不能确定〖备选习题〗:A 组 1、已知函数f(x)在定义域M内为增函数,且f(x)>0,则下列函数在M内不是增函数的是( ) A.y=4+3f(x) B.y=[f(x)]2 C. D.2 、 设是上 的 减 函 数 , 则的 单 调 递 减 区 间 为 . 3、设函数在R上是减函数,则有 A. B. C. D.4.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?B 组 已知是定义在上的增函数,且 (1)求的值; (2)若,解不等式〖课堂感悟〗: