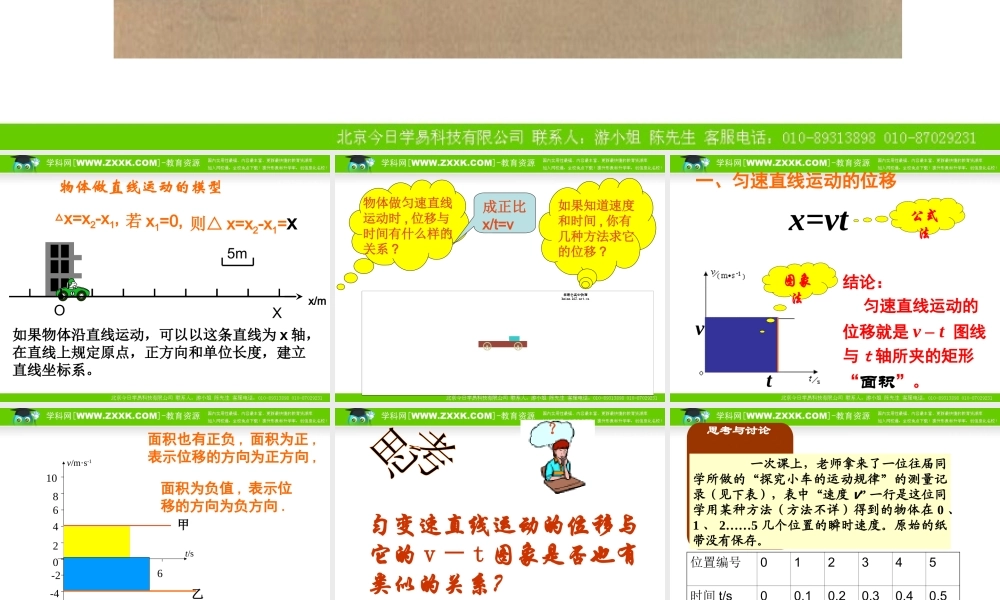
如果物体沿直线运动,可以以这条直线为 x 轴,在直线上规定原点,正方向和单位长度,建立直线坐标系。XO5mx/m物体做直线运动的模型△x=x2-x1, 若 x1=0, 则△ x=x2-x1=x 物体做匀速直线运动时 , 位移与时间有什么样的关系 ?如果知道速度和时间 , 你有几种方法求它的位移 ?成正比x/t=v 一、匀速直线运动的位移x=vt v t 结论: 匀速直线运动的位移就是 v – t 图线与 t 轴所夹的矩形“面积”。 公式法图象法 v/m·s-1t/s2641083 45 6021甲-2-4x面积也有正负 , 面积为正 ,表示位移的方向为正方向 ,面积为负值 , 表示位移的方向为负方向 .乙X 甲X 乙 匀变速直线运动的位移与它的 v - t 图象是否也有类似的关系?? 思考与讨论 一次课上,老师拿来了一位往届同学所做的“探究小车的运动规律”的测量记录(见下表),表中“速度 v” 一行是这位同学用某种方法(方法不详)得到的物体在 0 、1 、 2……5 几个位置的瞬时速度。原始的纸带没有保存。位置编号012345时间 t/s00.10.20.30.40.5速度 (m/s2) 0.38 0.63 0.88 1.11 1.38 1.62 以下是关于这个问题的讨论。老师:能不能根据表中的数据,用最简便的方法估算实验中小车从位置 0 到位置 5 的位移?学生 A :能。可以用下面的办法估算: x = 0.38×0.1 + 0.63×0.1 + 0.88×0.1 + 1.11×0.1 + 1.38×0.1 = ……思考与讨论 思考与讨论学生 B :这个办法不好。从表中看出,小车的速度在不断增加, 0.38 只是 0 时刻的瞬时速度,以后的速度比这个数值大。用这个数值乘以 0.1 s ,得到的位移比实际位移要小。后面的几项也有同样的问题。 学生 A :老师要求的是“估算”,这样做是可以的。 老师:你们两个人说得都有道理。这样做的确会带来一定误差,但在时间间隔比较小、精确程度要求比较低的时候,可以这样估算。 要提高估算的精确程度,可以有多种方法。其中一个方法请大家考虑:如果当初实验时时间间隔不是取 0.1 s ,而是取得更小些,比如 0.06 s ,同样用这个方法计算,误差是不是会小一些?如果取 0.04 s 、 0.02 s …… 误差会怎样? 欢迎大家发表意见。思考与讨论 科学思想方法:先把过程无限分割 ,以“不变”近似代替“变” , 然后再进行累加的思想 。这个材料中体现了什么科学思想?此科学思想方法能否应用到匀变速直线运动的v-t 图象上?思考 2思考 3 v/m/s02040510...