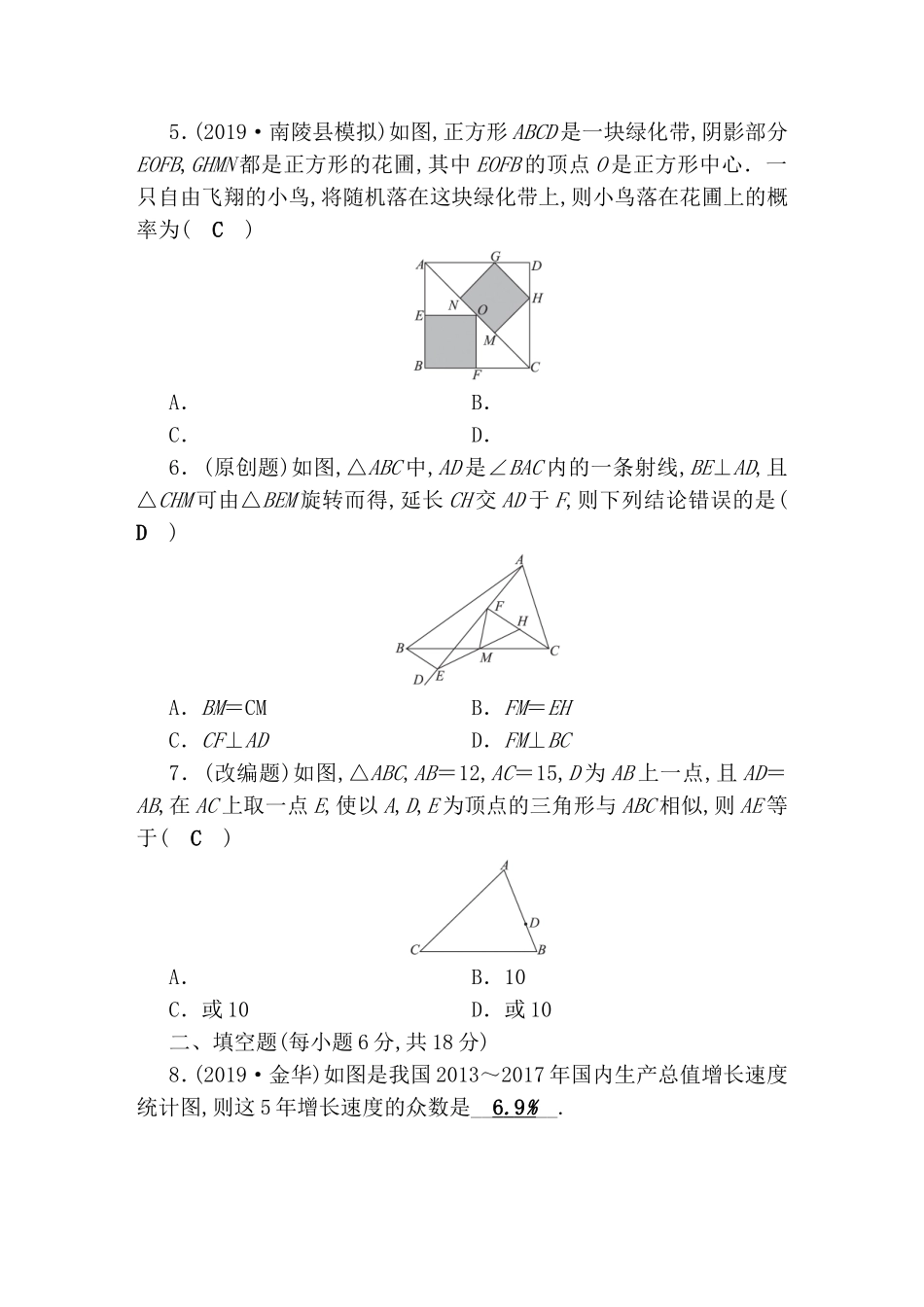
阶段性测试卷(三)(考查内容:图形与变换、统计与概率时间:45分钟满分:100分)一、选择题(每小题6分,共42分)1.(2019·广州)如图所示的几何体是由4个相同的小正方体搭成的,它的主视图是(B)ABCD2.(2019·淮南期末)下列图形中不是轴对称图形的是(A)ABCD3.甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是(B)A.掷一枚正六面体的骰子,出现1点的概率B.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率C.抛一枚硬币,出现正面的概率D.任意写一个整数,它能被2整除的概率4.如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连接AC′交A′C于D,则△C′DC的面积为(C)A.10B.8C.6D.45.(2019·南陵县模拟)如图,正方形ABCD是一块绿化带,阴影部分EOFB,GHMN都是正方形的花圃,其中EOFB的顶点O是正方形中心.一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为(C)A.B.C.D.6.(原创题)如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是(D)A.BM=CMB.FM=EHC.CF⊥ADD.FM⊥BC7.(改编题)如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=AB,在AC上取一点E,使以A,D,E为顶点的三角形与ABC相似,则AE等于(C)A.B.10C.或10D.或10二、填空题(每小题6分,共18分)8.(2019·金华)如图是我国2013~2017年国内生产总值增长速度统计图,则这5年增长速度的众数是__6.9%__.9.(改编题)已知,如图在△ABC中,DE∥BC,=,则=__1∶4__.10.(改编题)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值为____.三、解答题(共40分)11.(10分)(2019·青岛)小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4,5,6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.解:不公平.理由如下:方法1:画树状图如下:由树状图可知,共9种等可能的结果,其中和为偶数有5种结果,奇数有4种结果,∴P(小明获胜)=,P(小亮获胜)=,∴不公平.方法2:列表如下:456489105910116101112由表格可知,共9种等可能的结果,其中和为偶数有5种结果,奇数有4种结果,∴P(小明获胜)=,P(小亮获胜)=,∴不公平.12.(14分)(2019·安徽模拟)如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.(1)画出△ABC关于直线l成轴对称的△A0B0C0;(2)画出将△A0B0C0向上平移1个单位得到的△A1B1C1;(3)以格点O为位似中心,将△A1B1C1作位似变换,将其放大到原来的两倍,得到△A2B2C2.解:(1)如图所示:△A0B0C0,即为所求;(2)如图所示:△A1B1C1,即为所求;(3)如图所示:△A2B2C2,即为所求.13.(16分)(2019·安庆一模)在等腰直角△ABC中,∠ACB=90°,AC=BC,点P在斜边AB上(AP>BP).作AQ⊥AB,且AQ=BP,连结CQ(如图1).(1)求证:△ACQ≌△BCP;(2)延长QA至点R,使得∠RCP=45°,RC与AB交于点H,如图2.①求证:CQ2=QA·QR;②判断三条线段AH,HP,PB的长度满足的数量关系,并说明理由.(1)证明:∵∠ACB=90°,AC=BC,∴∠CAB=∠B=45°,又∵AQ⊥AB,∴∠QAC=∠CAB=45°=∠B,在△ACQ和△BCP中,∴△ACQ≌△BCP(SAS);(2)解:①由(1)知△ACQ≌△BCP,则∠QCA=∠PCB,∵∠RCP=45°,∴∠ACR+∠PCB=45°,∴∠ACR+∠QCA=45°,即∠QCR=45°=∠QAC,又∠Q为公共角,∴△CQR∽△AQC,∴=,∴CQ2=QA·QR;②AH2+PB2=HP2.理由:如图,连接QH,由(1)(2)题知:∠QCH=∠PCH=45°,CQ=CP,又∵CH是△QCH和△PCH的公共边,∴△QCH≌△PCH(SAS),∴HQ=HP,∵在Rt△QAH中,QA2+AH2=HQ2,又由(1)知:QA=PB,∴AH2+PB2=HP2.