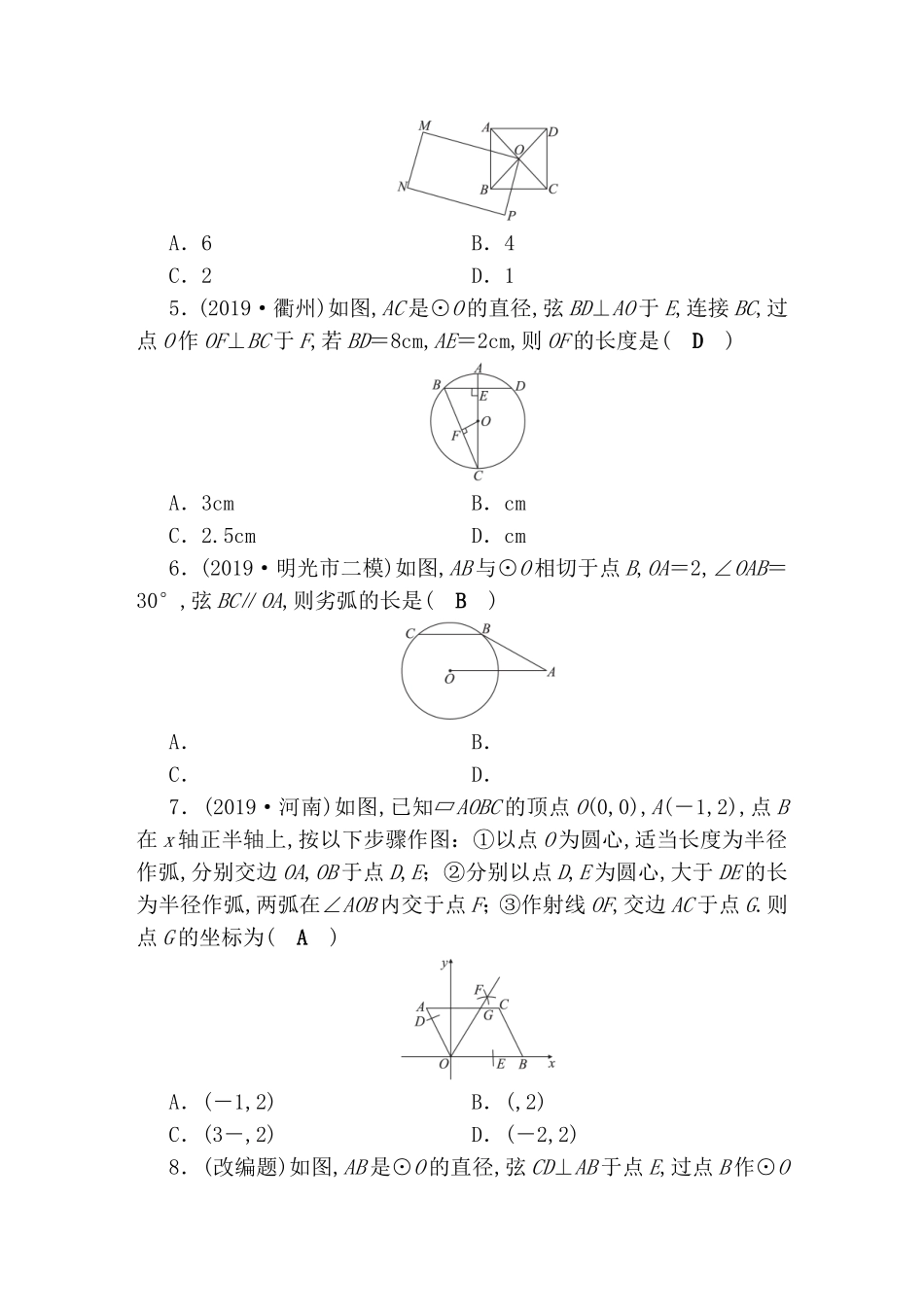
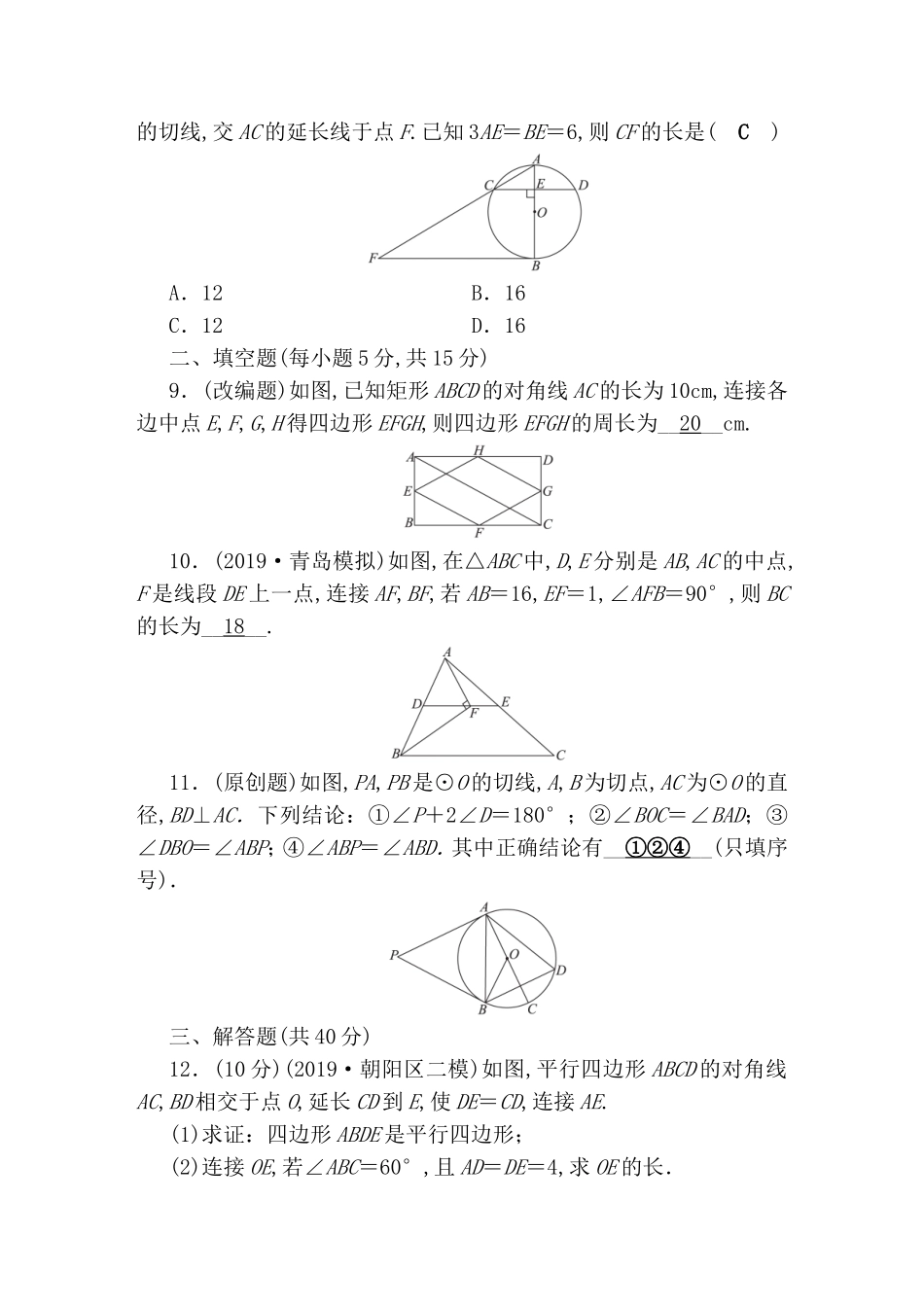
阶段性测试卷(二)(考查内容:三角形、四边形、圆时间:45分钟满分:100分)一、选择题(每小题5分,共40分)1.(改编题)如图,AB∥CD,CE交AB于点F.∠A=20°,∠E=30°,则∠C的度数为(A)A.50°B.55°C.60°D.65°2.(2019·蜀山区二模)如图,平行四边形ABCD中,∠ABC的角平分线交边CD于点E,∠A=130°,则∠BEC的度数是(B)A.20°B.25°C.30°D.50°3.(2019·宿州月考)在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是(D)A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形4.(改编题)正方形ABCD的边长为2,对角线相交于点O,点O又是长方形MNPO的一个顶点,且OM=4,OP=2,长方形绕O点转动的过程中,长方形与正方形重叠部分的面积等于(D)A.6B.4C.2D.15.(2019·衢州)如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是(D)A.3cmB.cmC.2.5cmD.cm6.(2019·明光市二模)如图,AB与⊙O相切于点B,OA=2,∠OAB=30°,弦BC∥OA,则劣弧的长是(B)A.B.C.D.7.(2019·河南)如图,已知▱AOBC的顶点O(0,0),A(-1,2),点B在x轴正半轴上,按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.则点G的坐标为(A)A.(-1,2)B.(,2)C.(3-,2)D.(-2,2)8.(改编题)如图,AB是⊙O的直径,弦CD⊥AB于点E,过点B作⊙O的切线,交AC的延长线于点F.已知3AE=BE=6,则CF的长是(C)A.12B.16C.12D.16二、填空题(每小题5分,共15分)9.(改编题)如图,已知矩形ABCD的对角线AC的长为10cm,连接各边中点E,F,G,H得四边形EFGH,则四边形EFGH的周长为__20__cm.10.(2019·青岛模拟)如图,在△ABC中,D,E分别是AB,AC的中点,F是线段DE上一点,连接AF,BF,若AB=16,EF=1,∠AFB=90°,则BC的长为__18__.11.(原创题)如图,PA,PB是⊙O的切线,A,B为切点,AC为⊙O的直径,BD⊥AC.下列结论:①∠P+2∠D=180°;②∠BOC=∠BAD;③∠DBO=∠ABP;④∠ABP=∠ABD.其中正确结论有__①②④__(只填序号).三、解答题(共40分)12.(10分)(2019·朝阳区二模)如图,平行四边形ABCD的对角线AC,BD相交于点O,延长CD到E,使DE=CD,连接AE.(1)求证:四边形ABDE是平行四边形;(2)连接OE,若∠ABC=60°,且AD=DE=4,求OE的长.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵DE=CD,∴AB綊DE,∴四边形ABDE是平行四边形;(2)解:∵AD=DE=4,∴AD=AB=4,∴▱ABCD是菱形,∴AB=BC,AC⊥BD,BO=BD,∠ABO=∠ABC,又∵∠ABC=60°,∴∠ABO=30°,在Rt△ABO中,AO=AB·sin∠ABO=2,BO=AB·cos∠ABO=2,∴BD=4,∵四边形ABDE是平行四边形,∴AE∥BD,AE=BD=4,又∵AC⊥BD,∴AC⊥AE,在Rt△AOE中,OE==2.13.(15分)(2019·霍邱县二模)已知:如图,四边形ABCD是⊙O的内接四边形,直径DG交边AB于点E,AB,DC的延长线相交于点F.连接AC,若∠ACD=∠BAD.(1)求证:DG⊥AB;(2)若AB=6,tan∠FCB=3,求⊙O半径.(1)证明:连接AG,∵∠ACD与AGD是同弦所对圆周角,∴∠ACD=∠AGD,∵∠ACD=∠BAD,∴∠BAD=∠AGD,∵DG为⊙O的直径,A为圆周上一点,∴∠DAG=90°,∴∠BAD+∠BAG=90°,∴∠AGD+∠BAG=90°,∴∠AEG=90°,即DG⊥AB;(2)解:∵四边形ABCD是⊙O的内接四边形,∴∠FCB=∠BAD,∵tan∠FCB=3,∴tan∠BAD==3,连接OA,由垂径定理得AE=AB=3,∴DE=9,在Rt△OEA中,OE2+AE2=OA2,设⊙O半径为r,则有(9-r)2+32=r2,解得,r=5,∴⊙O半径为5.14.(15分)(2019·安徽四模)如图,⊙O的直径AD长为6,AB是弦,∠DAB=30°,CD∥AB,且CD=.(1)求∠C的度数;(2)求证:BC是⊙O的切线.(1)解:如图,连接BD,∵AD为圆O的直径,∴∠ABD=90°,∴BD=AD=3,∵CD∥AB,∠ABD=90°,∴∠CDB=∠ABD=90°,在Rt△CDB中,tanC===,∴∠C=60°;(2)证明:连接OB,∵BD=3,AD=6,∴∠A=30°,∵OA=OB,∴∠OBA=∠A=30°,∵CD∥AB,∠C=60°,∴∠ABC=180°-∠C=120°,∴∠OBC=∠ABC-∠ABO=120°-30°=90°,∴OB⊥BC,∴BC为圆O的切线.