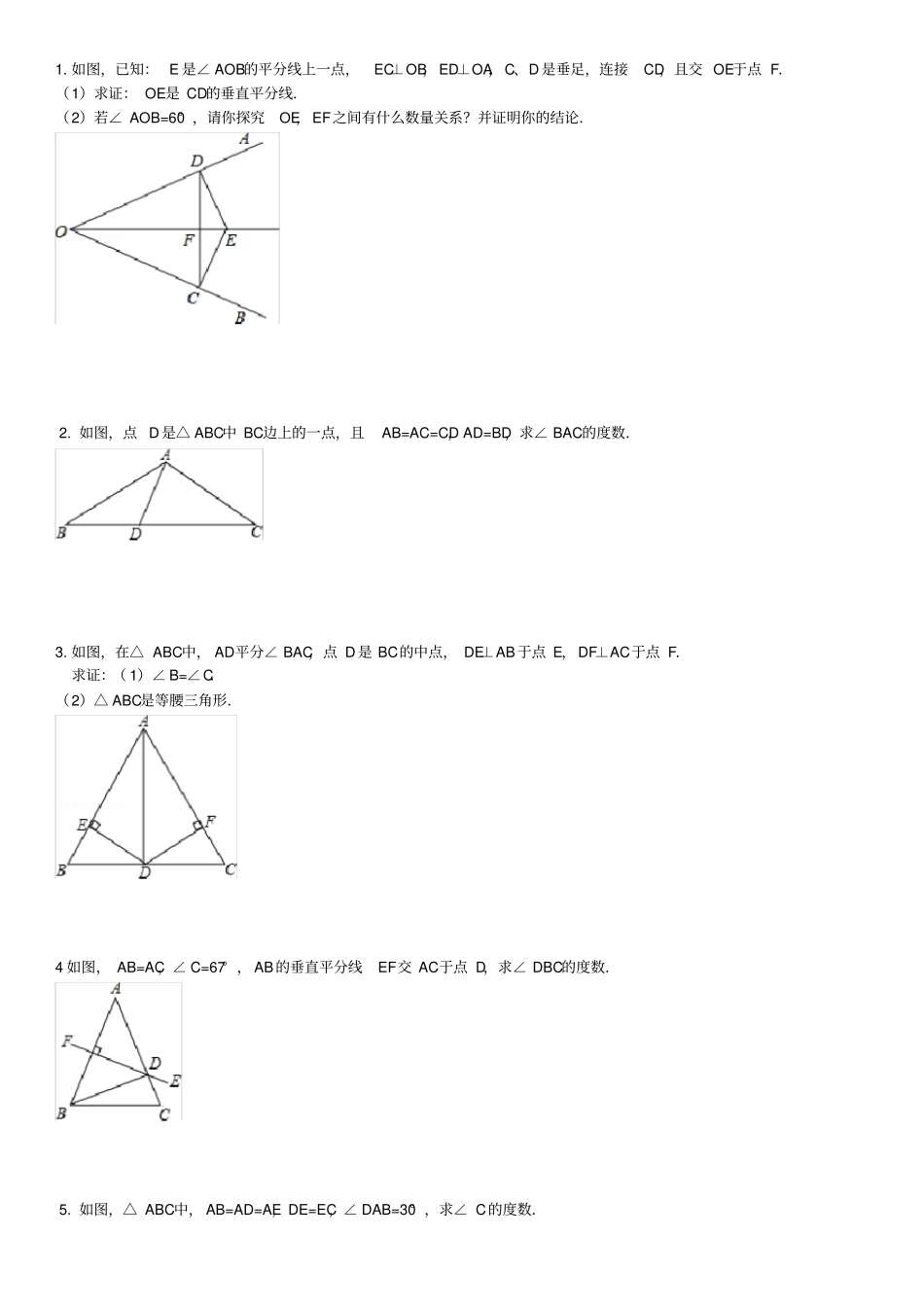
三角形证明题练习1.如图,在△ABC中,∠C=90°,AB的垂直平分线交AB与D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是()2.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有()3.如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=()4.如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为()5.如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为()6.如图,点O在直线AB上,射线OC平分∠AOD,若∠AOC=35°,则∠BOD等于()7.如图,在△ABC中,∠ACB=90°,BA的垂直平分线交BC边于D,若AB=10,AC=5,则图中等于60°的角的个数是()8.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是()9.在Rt△ABC中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于()A.13B.10C.12D.5A.5个B.4个C.3个D.2个A.4:3B.3:4C.16:9D.9:16A.70°B.80°C.40°D.30°A.30°B.36°C.40°D.45°A.145°B.110°C.70°D.35°A.2B.3C.4D.5A.2B.3C.6D.不能确定A.3.8cmB.7.6cmC.11.4cmD.11.2cm10.△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等;∠A=40°,则∠BOC=()11.如图,已知点P在∠AOB的平分线OC上,PF⊥OA,PE⊥OB,若PE=6,则PF的长为()12.如图,△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1cm,△ACD的周长为12cm,则△ABC的周长是()13.如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于()14.如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是()15.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则()16.如图,已知在△ABC中,AB=AC,D为BC上一点,BF=CD,CE=BD,那么∠EDF等于()17.如图,在△ABC中,AB=AC,AD平分∠BAC,那么下列结论不一定成立的是()三角形证明中经典题2A.110°B.120°C.130°D.140°A.2B.4C.6D.8A.13cmB.14cmC.15cmD.16cmA.50°B.75°C.80°D.105°A.AC=A′C′,BC=B′C′B.∠A=∠A′,AB=A′B′C.AC=A′C′,AB=A′B′D.∠B=∠B′,BC=B′C′A.BC>PC+APB.BC<PC+APC.BC=PC+APD.BC≥PC+APA.90°﹣∠AB.90°﹣∠AC.180°﹣∠AD.45°﹣∠AA.△ABD≌△ACDB.AD是△ABC的高线C.AD是△ABC的角平分线D.△ABC是等边三角形1.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.(1)求证:OE是CD的垂直平分线.(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.2.如图,点D是△ABC中BC边上的一点,且AB=AC=CD,AD=BD,求∠BAC的度数.3.如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.求证:(1)∠B=∠C.(2)△ABC是等腰三角形.4如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数.5.如图,△ABC中,AB=AD=AE,DE=EC,∠DAB=30°,求∠C的度数.6.阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边”,如图,在△ABC中,已知∠ABC和∠ACB的平分线上交于点F,过点F作BC的平行线分别交AB、AC于点D、E,请你用“等角对等边”的知识说明DE=BD+CE.7.如图,AD是△ABC的平分线,DE,DF分别垂直AB、AC于E、F,连接EF,求证:△AEF是等腰三角形.2015年05月03日初中数学三角形证明组卷参考答案与试题解析一.选择题(共20小题)1.(2015?涉县模拟)如图,在△ABC中,∠C=90°,AB的垂直平分线交AB与D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是()A.13B.10C.12D.5考点:线段垂直平分线的性质.分析:先根据勾股定理求出AE=13,再由DE是线段AB的垂直平分线,得出BE=AE=13.解答:解: ∠C=90°,∴AE=, DE是线段AB的垂直平分线,∴BE=AE=13;故选:A.点评:本题考查了勾股定理和线段垂直平分线的性质;利用勾股定理求出AE是解题的关键.2.(2015?淄博...