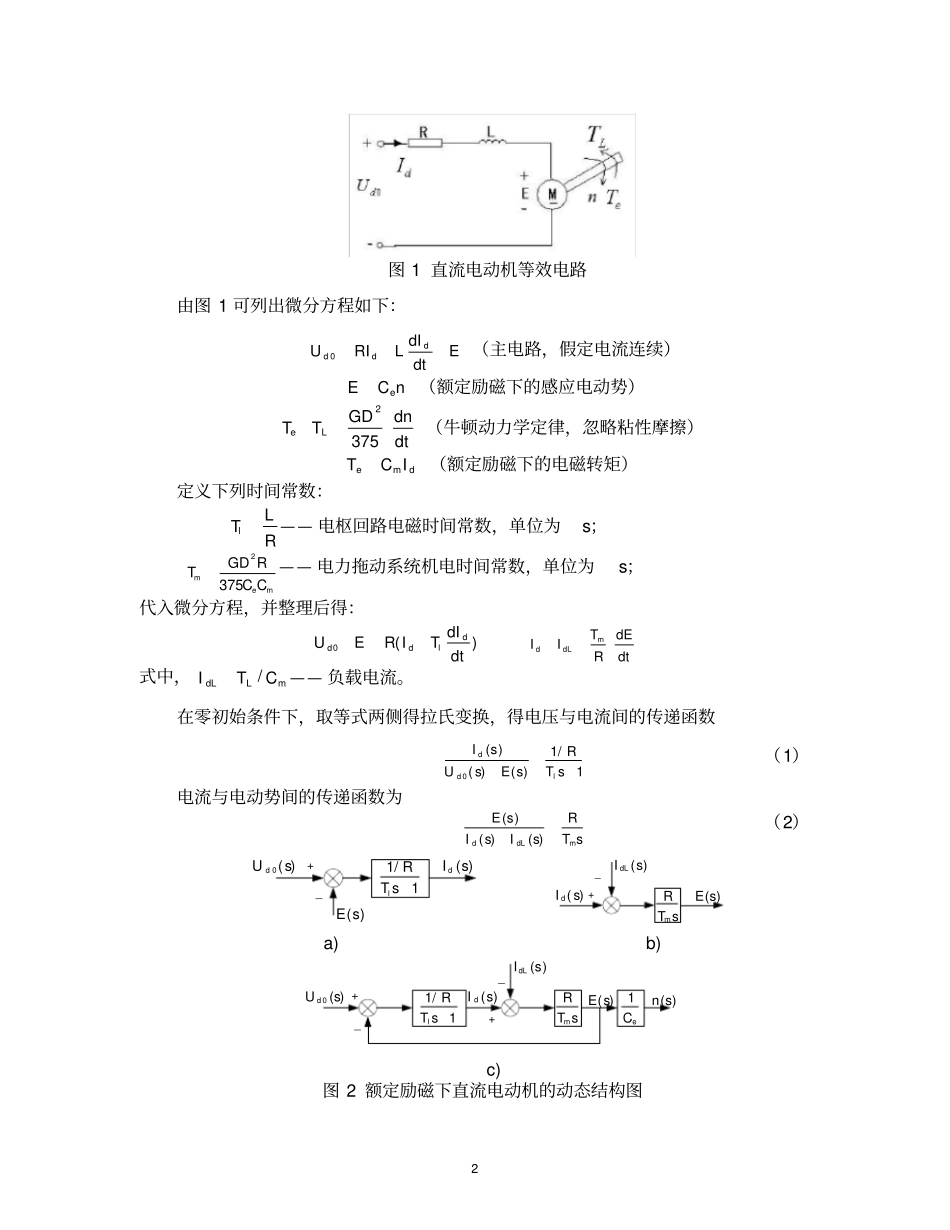
控制系统数字仿真与CAD实验指导书张晓华编哈尔滨工业大学电气工程系2006年3月1“双闭环控制直流电动机调速系统”数字仿真实验一、实验目的1.熟悉Matlab/Simulink仿真环境;2.掌握Simulink图形化建模方法;3.验证“直流电动机转速/电流双闭环PID控制方案”的有效性。二、实验内容1.“双闭环直流电动机调速系统”的建模2.电流环/调节器设计3.电流环动态跟随性能仿真实验4.转速环/调节器设计5.转速环动态抗扰性能仿真实验6.系统动态性能分析(给出仿真实验结果与理论分析结果的对比/分析/结论)三、实验步骤1、系统建模A.控制对象的建模建立线性系统动态数学模型的基本步骤如下:(1)根据系统中各环节的物理定律,列写描述据该环节动态过程的微分方程;(2)求出各环节的传递函数;(3)组成系统的动态结构图并求出系统的传递函数。下面分别建立双闭环调速系统各环节的微分方程和传递函数。B.额定励磁下的直流电动机的动态数学模型图1给出了额定励磁下他励直流电机的等效电路,其中电枢回路电阻R和电感L包含整流装置内阻和平波电抗器电阻与电感在内,规定的正方向如图所示。2图1直流电动机等效电路由图1可列出微分方程如下:0ddddIURILEdt(主电路,假定电流连续)eECn(额定励磁下的感应电动势)2375eLGDdnTTdt(牛顿动力学定律,忽略粘性摩擦)emdTCI(额定励磁下的电磁转矩)定义下列时间常数:lLTR——电枢回路电磁时间常数,单位为s;2375memGDRTCC——电力拖动系统机电时间常数,单位为s;代入微分方程,并整理后得:0()dddldIUERITdtmddLTdEIIRdt式中,/dLLmITC——负载电流。在零初始条件下,取等式两侧得拉氏变换,得电压与电流间的传递函数0()1/()()1ddlIsRUsEsTs(1)电流与电动势间的传递函数为()()()ddLmEsRIsIsTs(2)0()dUs+_()Es1/1lRTs()dIs_+()dIs()dLIsmRTs()Esa)b)mRTs1/1lRTs1eC+__+0()dUs()dIs()dLIs()Es()nsc)图2额定励磁下直流电动机的动态结构图3a)式(1)的结构图b)式(2)的结构图c)整个直流电动机的动态结构图C.晶闸管触发和整流装置的动态数学模型在分析系统时我们往往把它们当作一个环节来看待。这一环节的输入量是触发电路的控制电压Uct,输出量是理想空载整流电压Ud0。把它们之间的放大系数Ks看成常数,晶闸管触发与整流装置可以看成是一个具有纯滞后的放大环节,其滞后作用是由晶闸管装置的失控时间引起的。下面列出不同整流电路的平均失控时间:表1各种整流电路的平均失控时间(f=50Hz)整流电路形式平均失控时间Ts/ms单相半波10单相桥式(全波)5三相全波3.33三相桥式,六相半波1.67用单位阶跃函数来表示滞后,则晶闸管触发和整流装置的输入输出关系为01()dsctsUKUtT按拉氏变换的位移定理,则传递函数为0()()sTsdsctUsKeUs(3)由于式(3)中含有指数函数sTse,它使系统成为非最小相位系统,分析和设计都比较麻烦。为了简化,先将sTse按台劳级数展开,则式(3)变成02233()11()12!3!ssTsdsssTsctsssUsKKKeUseTsTsTsL考虑到Ts很小,忽略其高次项,则晶闸管触发和整流装置的传递函数可近似成一阶惯性环节0()()1dsctsUsKUsTs(4)其结构图如图3所示。4()ctUs0()dUssTssKe()ctUs0()dUs1ssKTsa)b)图3晶闸管触发和整流装置的动态结构图a)准确的结构图b)近似的结构图D.比例放大器、测速发电机和电流互感器的动态数学模型比例放大器、测速发电机和电流互感器的响应都可以认为是瞬时的,因此它们的放大系数也就是它们的传递函数,即()()ctpnUsKUs(5)()()nUsns(6)()()idUsIs(7)E.双闭环控制直流电动机调速系统的动态数学模型根据以上分析,可得双闭环控制系统的动态结构图如下1/1lRTsmRTs1eC1ssKTs()ACRWs()ASRWsnUiUctU0dUdLIdInnUiU____图4双闭环控制系统的动态结构图2、实验系统参数系统中采用三相桥式晶闸管整流装置,基本参数如下:直流电动机:220V,13.6A,1480r/min,eC=0.131V/(r/min),允许过载倍数λ=1.5。晶闸管装置:76sK。电枢回路总电阻:R=6.58Ω。5时间常数:lT=0.018s,mT=0.25s。反馈系数:α=0.00337V/(r/min),β=0.4V/A。反馈滤波时间常数:oiT=0.005s,onT=0.005s。3.PID调节器参数设计设计多闭环控制系统的一般...