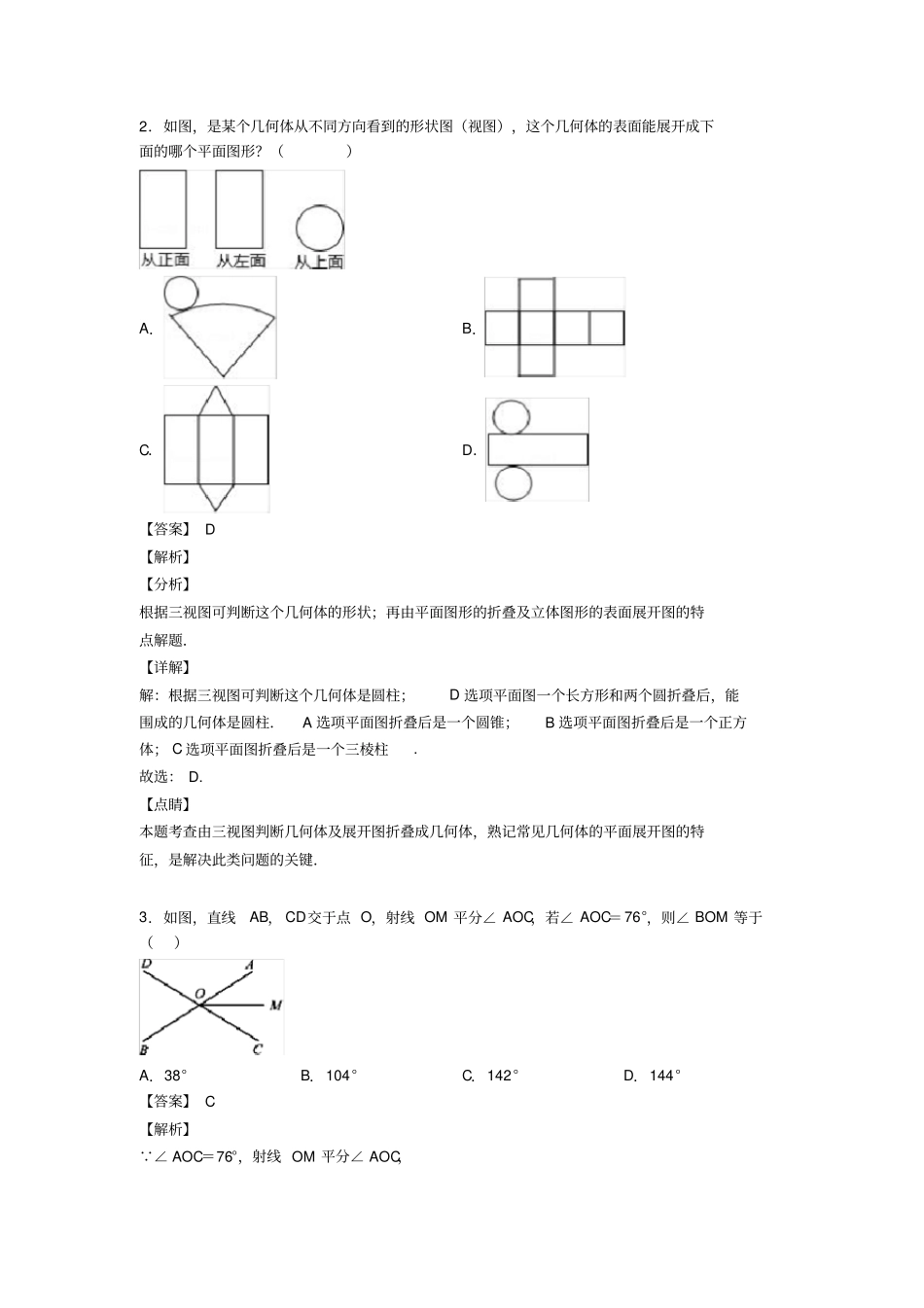
初中数学几何图形初步知识点总复习附答案一、选择题1.如图,已知ABC的周长是21,OB,OC分别平分ABC和ACB,ODBC^于D,且4OD,则ABC的面积是()A.25米B.84米C.42米D.21米【答案】C【解析】【分析】根据角平分线的性质可得点O到AB、AC、BC的距离为4,再根据三角形面积公式求解即可.【详解】连接OA OB,OC分别平分ABC和ACB,ODBC^于D,且4OD∴点O到AB、AC、BC的距离为4∴ABCAOCOBCABOSSSS△△△△142ABBCAC1421242(米)故答案为:C.【点睛】本题考查了三角形的面积问题,掌握角平分线的性质、三角形面积公式是解题的关键.2.如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?()A.B.C.D.【答案】D【解析】【分析】根据三视图可判断这个几何体的形状;再由平面图形的折叠及立体图形的表面展开图的特点解题.【详解】解:根据三视图可判断这个几何体是圆柱;D选项平面图一个长方形和两个圆折叠后,能围成的几何体是圆柱.A选项平面图折叠后是一个圆锥;B选项平面图折叠后是一个正方体;C选项平面图折叠后是一个三棱柱.故选:D.【点睛】本题考查由三视图判断几何体及展开图折叠成几何体,熟记常见几何体的平面展开图的特征,是解决此类问题的关键.3.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠AOC=76°,则∠BOM等于()A.38°B.104°C.142°D.144°【答案】C【解析】 ∠AOC=76°,射线OM平分∠AOC,∴∠AOM=12∠AOC=12×76°=38°,∴∠BOM=180°-∠AOM=180°-38°=142°,故选C.点睛:本题考查了对顶角相等的性质,角平分线的定义,准确识图是解题的关键.4.下列图形经过折叠不能围成棱柱的是().A.B.C.D.【答案】B【解析】试题分析:三棱柱的展开图为3个矩形和2个三角形,故B不能围成.考点:棱柱的侧面展开图.5.如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1,cm则该六棱柱的侧面积是()A.210824(3)cmB.2108123cmC.254243cmD.254123cm【答案】A【解析】【分析】设正六棱柱的底面边长为acm,高为hcm,分别表示出挪动前后所在矩形的长与宽,由题意列出方程求出a=2,h=9-23,再根据六棱柱的侧面积是6ah求解.【详解】解:设正六棱柱的底面边长为acm,高为hcm,如图,正六边形边长AB=acm时,由正六边形的性质可知∠BAD=30°,∴BD=12acm,AD=32acm,∴AC=2AD=3acm,∴挪动前所在矩形的长为(2h+23a)cm,宽为(4a+12a)cm,挪动后所在矩形的长为(h+2a+3a)cm,宽为4acm,由题意得:(2h+23a)-(h+2a+3a)=5,(4a+12a)-4a=1,∴a=2,h=9-23,∴该六棱柱的侧面积是6ah=6×2×(9-23)=210824(3)cm;故选:A.【点睛】本题考查了几何体的展开图,正六棱柱的性质,含30度角的直角三角形的性质;能够求出正六棱柱的高与底面边长是解题的关键.6.下面四个图形中,是三棱柱的平面展开图的是()A.B.C.D.【答案】C【解析】【分析】根据三棱柱的展开图的特点作答.【详解】A、是三棱锥的展开图,故不是;B、两底在同一侧,也不符合题意;C、是三棱柱的平面展开图;D、是四棱锥的展开图,故不是.故选C.【点睛】本题考查的知识点是三棱柱的展开图,解题关键是熟练掌握常见立体图形的平面展开图的特征.7.如图,有A,B,C三个地点,且ABBC,从A地测得B地在A地的北偏东43的方向上,那么从B地测得C地在B地的()A.北偏西43B.北偏西90C.北偏东47D.北偏西47【答案】D【解析】【分析】根据方向角的概念和平行线的性质求解.【详解】如图,过点B作BF∥AE,则∠DBF=∠DAE=43,∴∠CBF=∠DBC-∠DBF=90°-43°=47°,∴从B地测得C地在B地的北偏西47°方向上,故选:D.【点睛】此题考查方位角,平行线的性质,正确理解角度间的关系求出能表示点位置的方位角是解题的关键.8.某包装盒如下图所示,则在下列四种款式的纸片中,可以是该包装盒的展开图的是()A.B.C.D.【答案】A【解析】【分析】将展开图折叠还原成包装盒,即可判断正确选项.【详解】解:A、展开图折叠后如下图,与本题中包装盒相同,故本选项正确;B...