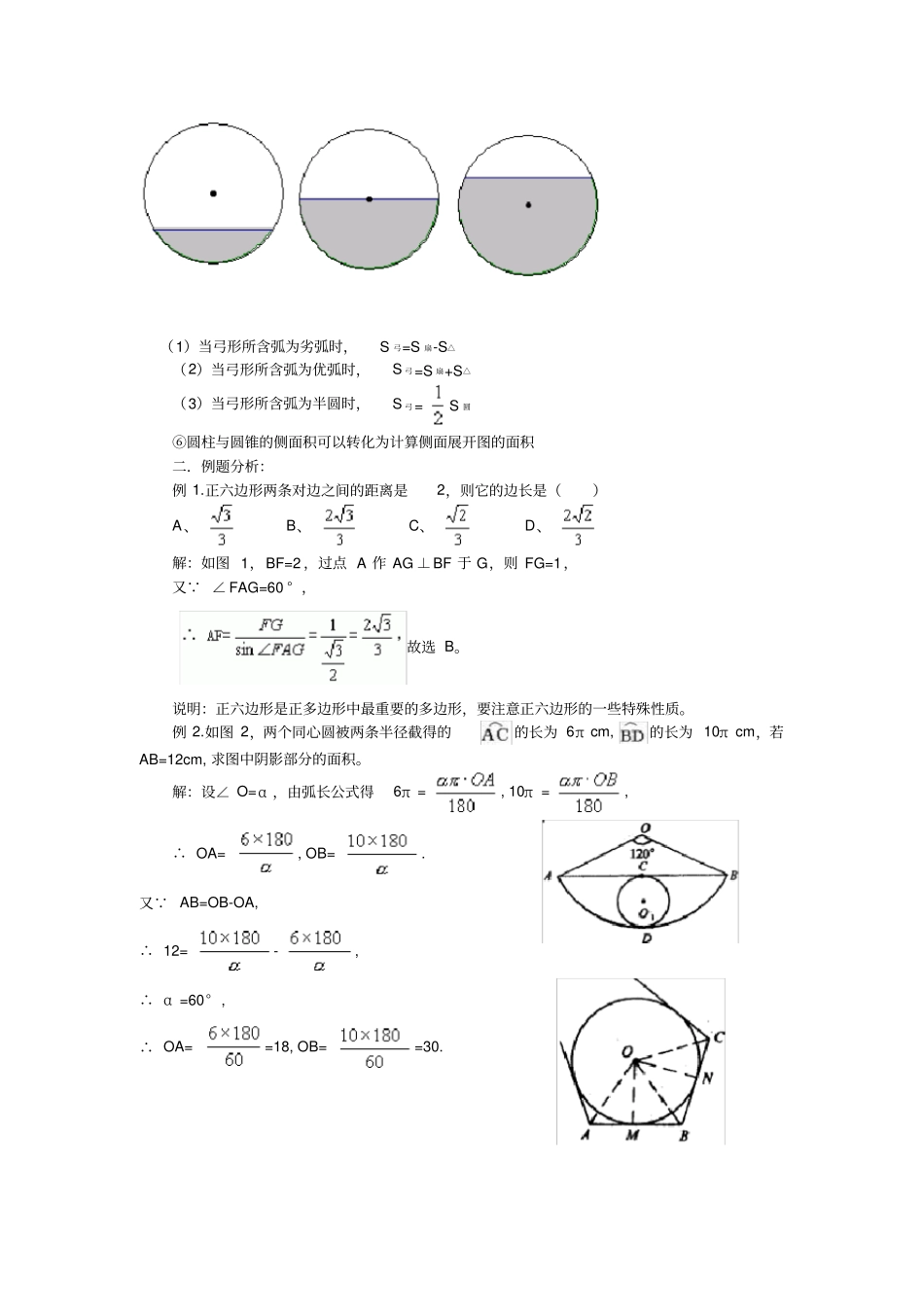
正多边形和圆(一)一.内容综述正多边形的有关计算方法、圆及简单组合图形的周长与面积的计算方法,是本单元的重点。实际上,这部分计算问题的解决大都是放在直角三角形(如下图△OAD)中解决的。掌握这些知识,一方面可以为进一步学习打好基础,另一方面这些知识在生产和生活中常常用到,所以要给予足够的重视。在正多边形的有关计算中,如果分别以αn、an、rn、Rn、Pn和Sn表示正n(n≥3,n为整数)边形的中心角、边长、边心距、半径、周长和面积,则有:①αn=;②an=2Rn·sin;③rn=Rn·cos;④+;⑤Pn=nan;⑥Sn=Pnrn;⑦Sn=nsin.(因为一个三角形的面积为:h·OB)注意两点:1、构造直角三角形(弦心距、边长的一半、半径组成的)求线段之间的关系等;2、准确记忆相关公式。在圆的有关计算中,如果用R表示圆的半径,n表示弧或弧所所对的圆心角的度数,L表示弧长,则有:①圆周长:C=2πR。②弧长:L=③圆面积:S=πR2④扇形面积:S扇形==LR⑤弓形面积可利用扇形面积与三角形面积的和或差来计算需根据不同的情况作出不同的处理:(1)当弓形所含弧为劣弧时,S弓=S扇-S△(2)当弓形所含弧为优弧时,S弓=S扇+S△(3)当弓形所含弧为半圆时,S弓=S圆⑥圆柱与圆锥的侧面积可以转化为计算侧面展开图的面积二.例题分析:例1.正六边形两条对边之间的距离是2,则它的边长是()A、B、C、D、解:如图1,BF=2,过点A作AG⊥BF于G,则FG=1,又 ∠FAG=60°,故选B。说明:正六边形是正多边形中最重要的多边形,要注意正六边形的一些特殊性质。例2.如图2,两个同心圆被两条半径截得的的长为6πcm,的长为10πcm,若AB=12cm,求图中阴影部分的面积。解:设∠O=α,由弧长公式得6π=,10π=,∴OA=,OB=.又 AB=OB-OA,∴12=-,∴α=60°,∴OA==18,OB==30.∴阴影部分的面积为:-==96π说明:本题主要考察弧长、扇形面积的有关计算,要熟记公式,正确运用。例3.求证圆的外切正多边形的面积等于其周长与圆的半径的积的一半.分析:外切正多边形可分成与边数相同个数的等腰三角形,其面积之和为正多边形的面积,而每个小三形的面积恰是边长与圆半径积的一半,故题易证.证明:设外切多边形周长为P,内切圆⊙O半径为R,连结O与正多边形的各顶点及切点,如图 OM⊥AB,ON⊥BC,⋯⋯,∴S△OAB=OM·AB=R·AB,S△OBC=ON·BC=R·BC⋯⋯,∴正多边形ABCD⋯⋯面积为S=R(AB+BC+⋯⋯)=R·P.说明:圆的外切(或内接)正多边形的周长.面积的计算要通过所分成的n个等腰三角形进行,这也是由复杂到简单的一种转化,象四边形的问题一样,正n边形的问题首先应转化为三角形的问题,转化是解决数学问题的关键。例4.已知如图⊙O1为含120°弧的弓形的直径最大的内切圆,求证:这个内切圆的周长等于弧长的。分析:欲证内切圆的周长和含此内切圆弓形的弧之间的关系,需求出:内切圆⊙O1的周长2πr,及弓形的弧AB的长,找到r与⊙O的半径R的关系,结论易证。证明:设⊙O1切弓形于C、D,OA=R,O1C=r, ∠AOB=120°,∴的长=×=πR,又 ∠OAB=(180°-120°)=30°,∴OC=OA=R,r=(OD-OC)=(R-R)=R,∴又⊙O1的周长=2πr=2π·R=πR,∴⊙O1的周长等于弧长的.例5.已知如图半径OA=6cm,C为OB的中点,∠AOB=120°,求阴影部分面积S阴影ABC.分析:欲求S阴影ABC,从图形上看是不规则图形,所以问题的关键是将不规则的图形转化为规则图形面积的和或差,观察图形会发现S阴影=S扇形OAB-S△ACO,故可求得.解:由图示可知S阴影ABC=S扇形-S△ACO,而S扇形OAB==12π(cm2),∴S△ACO=×6×3·sin60°=(cm2),∴S阴影ABC=(12π-)cm2.说明:求阴影部分的面积,最关键的就是将不规则图形的面积转化为规则图形的面积的和或差,以上为例,S阴影可以折分为S扇形OAB与SDAOC的差,也可以折分为SDABC与S弓形AB的和,但因为这两个面积,求起来较繁锁,所以到底用哪种方法,要有所选择。例6.如图,若正六边形的面积为6,求正六边形内切圆的内接正三角形的面积.分析:如下图,线段OC是正六边形的边心距,由内接正三边形的边长,则线段OC可以将两图形联系起来。解:如图,设AB是正六边形的一条边长,C点为切点,CD为正六边形内切⊙O的内接正三角形的一条边长,过O点作OE⊥CD于E,分别连结OA、OB、...