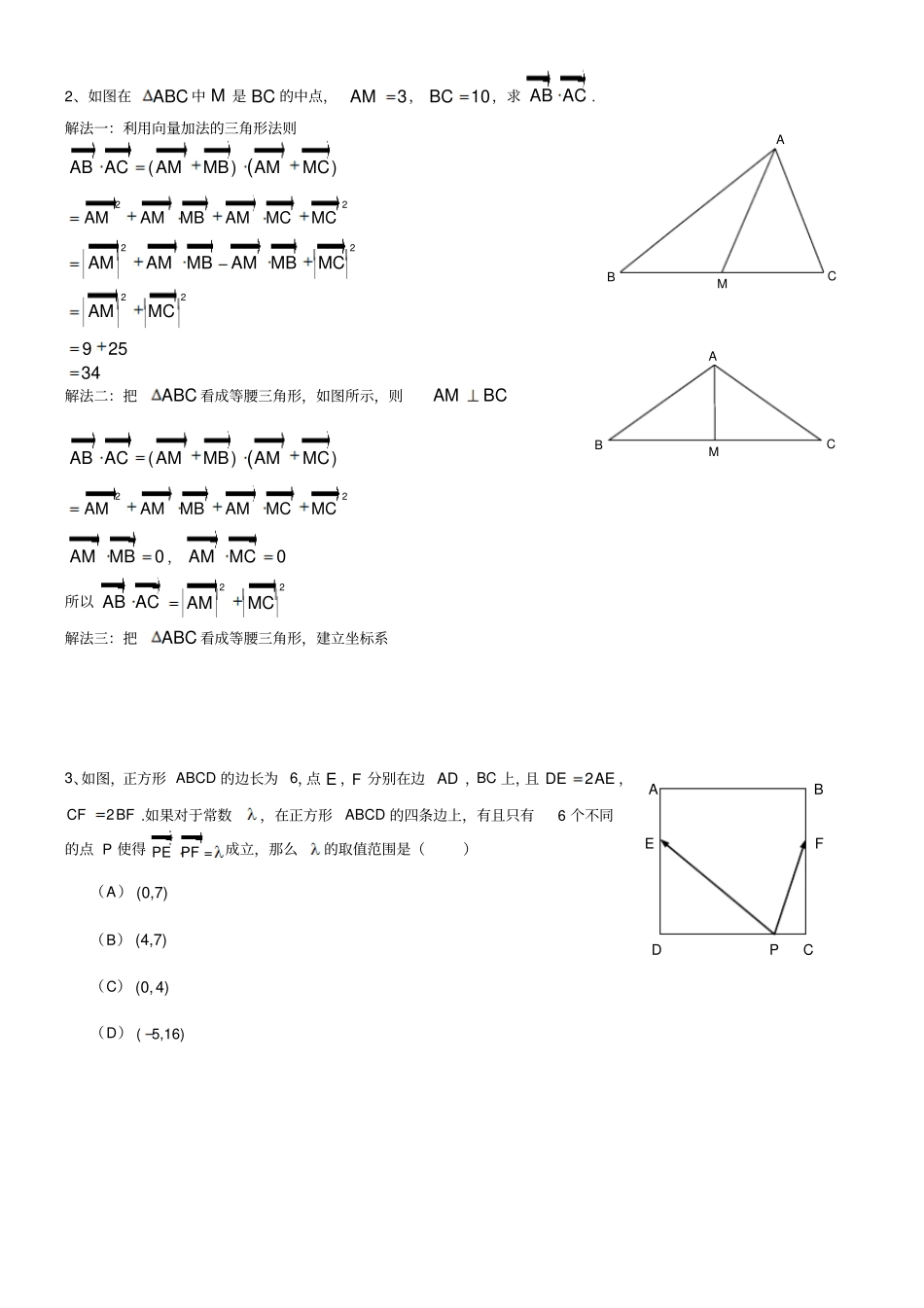
向量综合复习例1、已知OAa+2b,OB2a+4b,OC3a+6b(其中a、b是两个任意非零向量),证明:A、B、C三点共线.例2、在梯形ABCD中,//ADBC,2,6,4ABBCAD,AC与BD交于O点,设,ABADab用,ab表示OA.一、善于用坐标解决问题1、在边长为2的正方形ABCD中,,EF分别为BC和DC的中点,则AEAF()A.52B.32C.4D.2变式训练:如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序DABC沿线段DA,AB,BC运动到C点,在此过程中DECD的最大值是(A)A.0B.12C.1D.1ODCBACABDFE2、如图在ABC中M是BC的中点,3AM,10BC,求ABAC.解法一:利用向量加法的三角形法则())(ABACAMMBAMMC22AMAMMBAMMCMC22AMAMMBAMMBMC22AMMC92534解法二:把ABC看成等腰三角形,如图所示,则AMBC())(ABACAMMBAMMC22AMAMMBAMMCMC0AMMB,0AMMC所以ABAC22AMMC解法三:把ABC看成等腰三角形,建立坐标系3、如图,正方形ABCD的边长为6,点E,F分别在边AD,BC上,且2DEAE,2CFBF.如果对于常数,在正方形ABCD的四条边上,有且只有6个不同的点P使得=PEPF成立,那么的取值范围是()(A)(0,7)(B)(4,7)(C)(0,4)(D)(5,16)MCBAMCBAEFDPCABEDCBA4、向量(2,0)a,(,)bxy,若b与ba的夹角等于6,则b的最大值为()A.4B.23C.2D.433三角形中向量问题:1、P是ABC所在平面上一点,若PAPBPBPCPCPA,则P是ABC的A、外心B、内心C、重心D、垂心2、设O为ABC的外心,且满足OAOBOC,则ACB___________.3、在ABC中,点P满足()APtABAC,且BPAPCPAP,则ABC一定是()A.直角三角形B.等腰三角形C.等边三角形D.钝角三角形练习:1、设,ab是非零向量,若函数()()()fxxxabab的图象是一条直线,则必有()A.⊥abB.∥abC.||||abD.||||ab2、如图,在正方形ABCD中,4,ADE为DC上一点,且3DEEC,则ABAE()A.20B.16C.15D.123.已知两个不共线的向量,ab满足2xxy+=+abab,那么实数,xy的值分别是()(A)0,0(B)1,2(C)0,1(D)2,14.如图,用向量12,ee表示向量-ab为()(A)2124--ee(B)2142--ee(C)213-ee(D)213-+ee5.已知在四边形ABCD中满足:()()0ABACADDBADCD,则△ABC的形状是(A)等边三角形(B)等腰三角形(C)直角三角形(D)斜三角形6.已知向量(2a,1),(sinb,cos),且a∥b,则sin2cos5cos3sin=.7.下列四式不能化简为AD的是()A.BCCDAB)++(B.)+)+(+(CMBCMBADC.BMADMB-+D.CDOAOC+-8.已知|a|=3,|b|=4,(a+b)(a+3b)=33,则a与b的夹角为()A.30B.60C.120D.1509.a=(cos2x,sinx),b=(1,2sinx-1),x(,)2,若ab=25,则tan(x+4)等于()A.13B.27C.17D.2310.设向量a,b的长度分别为4和3,它们的夹角为060,则|a+b|等于()A.37B.13C.37D.1311.已知向量a、b均为单位向量,且ab.若(2a+3b)(ka-4b),则k的值为_____.12.定义两个向量a,b之间的运算“”为abab.若向量p(3,1),(2,0)q,则()ppq.13.已知2133OMOAOB=+,设AMAB=,那么实数的值是.bae2e114.(本小题满分7分)已知向量a,b满足a=(3,-1),b=(1,-3).(1)求a与b的夹角的余弦值;(2)求证:(a+b)⊥(a-b).15.(本小题满分8分)已知向量a、b满足1ab,a与b的夹角45.(1)求ab的值;(2)求2()+ab的值.16.(本小题共10分)已知向量(1,3)=a,(2,0)=-b.(Ⅰ)求向量-ab的坐标以及-ab与a的夹角;(Ⅱ)当1,1t时,求t-ab的取值范围.17.(本小题满分11分)已知向量(2,1)OA,(3,2)OB,(6,3)OCmm.(Ⅰ)若点,,ABC共线,求实数m的值;(Ⅱ)若△ABC为直角三角形,且A为直角,求实数m的值.18.如图,在直角三角形ABC中,斜边AB=4.设角A,ABC的面积为S.(1)试用表示S,并求S的最大值;(2)计算ABACBCBA的值.19.(本小题共13分)如图,平面内有三个向量OAOBOC,,,其中OA与OB的夹角为120°,OA与OC的夹角为30°,且1OAOB,23OC.(I)若将OC分解成分别与OA和OB共线的两个向量之和,在图中画出分解图示,并结合图示写出具体分解表达式;(II)若()OCOAOBR,,求和的值.ACBAOBC