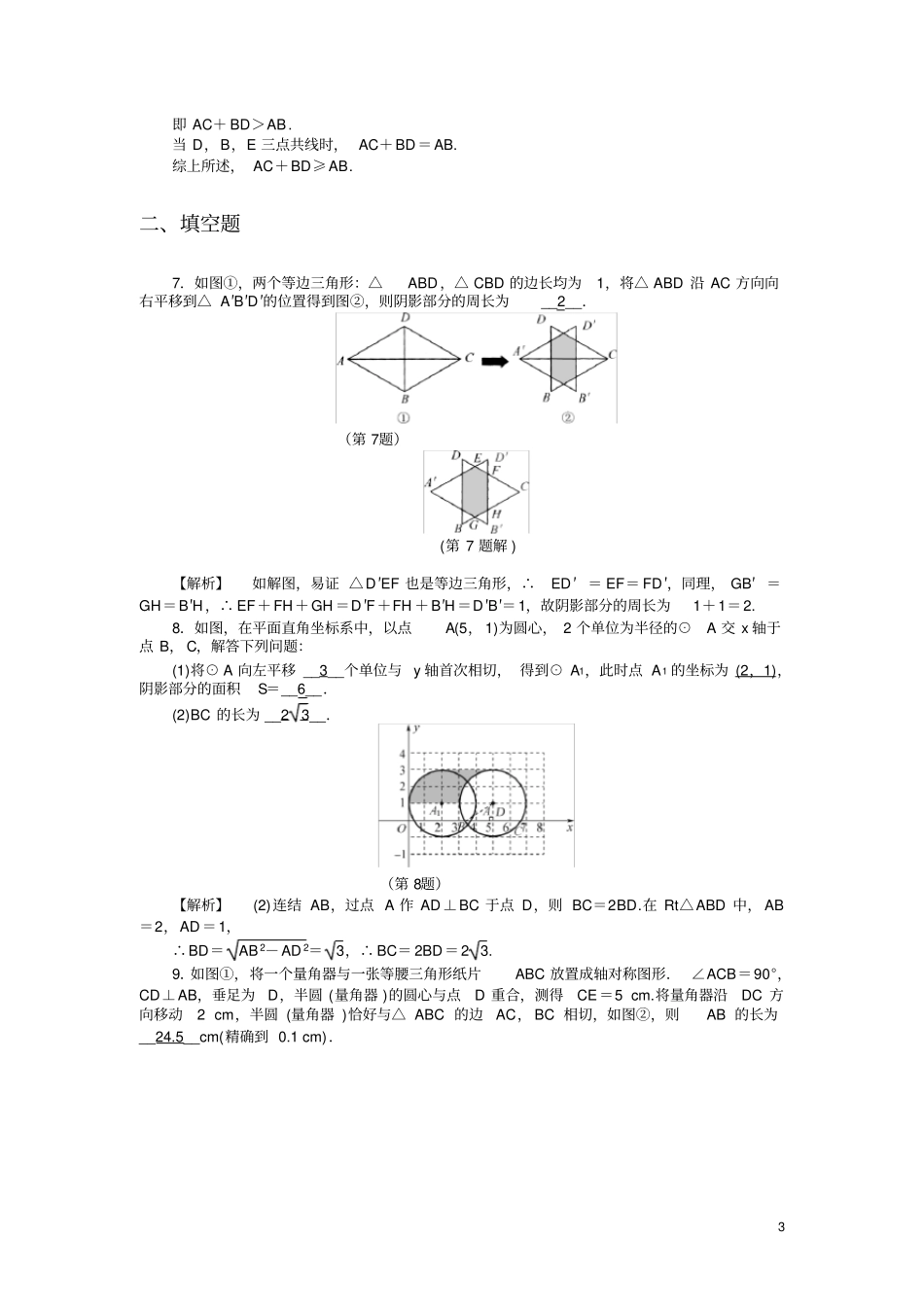
1义务教育基础课程初中教学资料课后强化训练30图形的平移一、选择题1.下列生活中的物体的运动情况可以看成平移的是(D)①摆动的钟摆;②在笔直的公路上行驶的汽车;③随风摆动的旗帜;④电风扇页的运动;⑤汽车玻璃上雨刷的运动;⑥从楼顶自由落下的球(球不旋转).A.①②B.①③④C.③④⑤D.②⑥【解析】①④⑤是旋转运动,错误;③是无规律运动,错误;只有②⑥可以看成平移,故选D.2.在6×6的方格中,将图①中的图形N平移后位置如图②所示,则图形N的平移方法中,正确的是(D)(第2题)A.向下移动1格B.向上移动1格C.向上移动2格D.向下移动2格【解析】观察图形可知:从图①到图②,可以将图形N向下移动2格.3.如图,把边长为2的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是(B)(第3题)A.18B.16C.12D.8【解析】 图①~图④的变化过程只是平移,∴每个基本图形的面积为4,∴图⑤的面积=4×4=16.(第4题)24.如图,等边三角形ABC沿射线BC向右平移到△DCE的位置,连结AD,BD,现有下列结论:①AD=BC;②BD,AC互相平分;③四边形ACED是菱形.其中正确结论的个数是(D)A.0B.1C.2D.3【解析】易知△ABC,△DCE是两个全等的等边三角形,∴∠ACB=∠DCE=60°,AC=CD,∴∠ACD=180°-∠ACB-∠DCE=60°,∴△ACD是等边三角形,∴AD=AC=BC,故①正确; AD=BC,AB=CD,∴四边形ABCD是平行四边形,∴BD,AC互相平分,故②正确;由①可得AD=AC=CE=DE,∴四边形ACED是菱形,故③正确.综上所述,①②③都正确.(第5题)5.如图,EF是△ABC的中位线,将△AEF沿中线AD的方向平移到△A1E1F1的位置,使E1F1与BC边重合.已知△AEF的面积为7,则图中阴影部分的面积为(B)A.7B.14C.21D.28【解析】 EF是△ABC的中线,∴EF綊12BC,∴S△AEF=14S△ABC=7,∴S△ABC=4S△AEF=4×7=28.又 S△A1E1F1=S△AEF,∴S阴影=28-7×2=14.(第6题)6.如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得,则AC+BD与AB的大小关系是(C)A.AC+BD>ABB.AC+BD=ABC.AC+BD≥ABD.无法确定【解析】由平移的性质知,AB与CE平行且相等,∴四边形ACEB是平行四边形,∴BE=AC.当B,D,E三点不共线时, AB∥CE,∴∠DCE=∠AOC=60°.又 CE=AB=CD,∴△CED是等边三角形.∴DE=CD=AB.根据三角形的三边关系知,BE+BD>DE,3即AC+BD>AB.当D,B,E三点共线时,AC+BD=AB.综上所述,AC+BD≥AB.二、填空题7.如图①,两个等边三角形:△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置得到图②,则阴影部分的周长为__2__.(第7题)(第7题解)【解析】如解图,易证△D′EF也是等边三角形,∴ED′=EF=FD′,同理,GB′=GH=B′H,∴EF+FH+GH=D′F+FH+B′H=D′B′=1,故阴影部分的周长为1+1=2.8.如图,在平面直角坐标系中,以点A(5,1)为圆心,2个单位为半径的⊙A交x轴于点B,C,解答下列问题:(1)将⊙A向左平移__3__个单位与y轴首次相切,得到⊙A1,此时点A1的坐标为(2,1),阴影部分的面积S=__6__.(2)BC的长为__23__.(第8题)【解析】(2)连结AB,过点A作AD⊥BC于点D,则BC=2BD.在Rt△ABD中,AB=2,AD=1,∴BD=AB2-AD2=3,∴BC=2BD=23.9.如图①,将一个量角器与一张等腰三角形纸片ABC放置成轴对称图形.∠ACB=90°,CD⊥AB,垂足为D,半圆(量角器)的圆心与点D重合,测得CE=5cm.将量角器沿DC方向移动2cm,半圆(量角器)恰好与△ABC的边AC,BC相切,如图②,则AB的长为__24.5__cm(精确到0.1cm).4(第9题)【解析】设量角器的半径为r,根据图②有3+r=2r,解得r=32+3,∴CD=5+r=8+32,∴AB=2CD=16+62≈24.5(cm).10.如图,在面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤进行裁剪和拼图.(第10题)第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ...