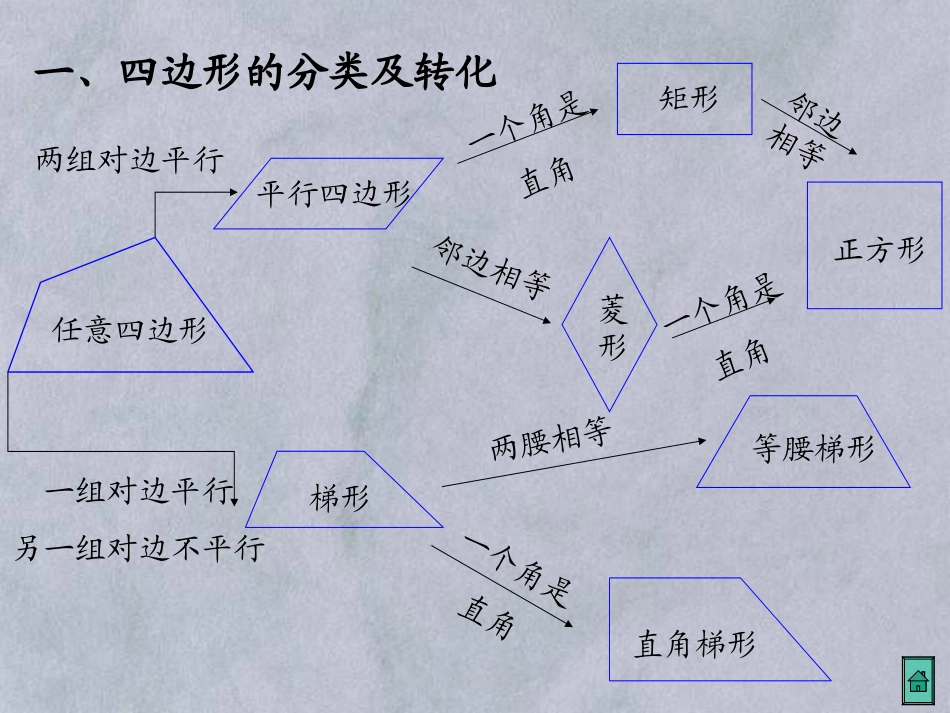
梅花香自苦寒来宝剑锋从磨砺出龙伏小学李涛任意四边形平行四边形矩形菱形正方形梯形等腰梯形直角梯形两组对边平行一个角是直角邻边相等邻边相等一个角是直角一个角是直角两腰相等一组对边平行另一组对边不平行一、四边形的分类及转化项目四边形对边角对角线对称性平行四边形矩形菱形正方形等腰梯形平行且相等平行且相等平行且四边相等平行且四边相等两底平行两腰相等对角相等邻角互补四个角都是直角同一底上的角相等对角相等邻角互补四个角都是直角互相平分互相平分且相等互相垂直平分,且每一条对角线平分一组对角相等互相垂直平分且相等,每一条对角线平分一组对角中心对称图形中心对称图形轴对称图形中心对称图形轴对称图形中心对称图形轴对称图形轴对称图形二、几种特殊四边形的性质:四边形条件平行四边形矩形菱形正方形等腰梯形三、几种特殊四边形的常用判定方法:1、定义:两组对边分别平行2、两组对边分别相等3、一组对边平行且相等4、对角线互相平分1、定义:有一外角是直角的平行四边形2、三个角是直角的四边形3、对角线相等的平行四边形1、定义:一组邻边相等的平行四边形2、四条边都相等的四边形3、对角线互相垂直的平行四边形1、定义:一组邻边相等且有一个角是直角的平行四边形2、有一组邻边相等的矩形3、有一个角是直角的菱形1、两腰相等的梯形2、在同一底上的两角相等的梯形3、对角线相等的梯形四、中心对称图形与中心对称的区别和联系中心对称图形:中心对称:如果把一个图形绕着某一点旋转180°后与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做对称中心。如果把一个图形绕着某一点旋转180°后与另一个图形重合,那么这两个图形关于这个点中心对称,这个点叫做对称中心。ABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDABCDC′A′B′ABCABCABCABCABCABCABCABCABCABCABCABCABCABCABCABCABCABCABC1、中心对称的两个图形是全等图形2、中心对称的两个图形的对称点连线通过对称中心,且被对称中心平分中心对称图形的对称点连线通过对称中心,且被对称中心平分oo五、有关定理:1、四边形的内角和等于,外角和等于。n边形的内角和等于,外角和等于。360°(n-2)·180°360°360°2、两条平行线之间的距离以及性质:平行线段两条平行线3、夹在两条平行线间的相等夹在间的垂线段相等AB两条平行线中,一条直线上任意一点到另一条直线的距离,叫这两条平行线的距离。ABCDL1L2如:ABCDL1L2如:4、一组平行线在一条直线上截得的线段相等,则在其它直线上截得的线段也。5、经过三角形一边的中点,且平行于另一边的直线,必定6、过梯形一腰的中点,且平行于底边的直线,必定。ABCDEF条件:ADBECF∥∥,AB=BC结论:DE=EFABCDE条件:在△ABC中,AD=BD,DEBC∥结论:AE=ECABFEDC条件:在梯形ABCD中,AE=DE,ABEF∥∥DC结论:BF=FC相等平分第三边平分另一腰7、三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半。ABCDEDEBC∥,DE=1/2BCADBCEF8、梯形中位线定理:梯形的中位线定理平行于两底,并且等于两底和的一半。EFADBC∥∥,EF=1/2(AD+BC)平移一腰作两高平移一对角线过梯形一腰中点和上底一端作直线延长两腰六、梯形问题中常添加的辅助线:七、选择题:(1)菱形ABCD的周长为20cm,∠ABC=120°,则对角线BD等于()(A)4cm(B)6cm(C)5cm(D)10cm(2)下列图形既是轴对称图形又是中心对称图形的是()(A)等腰三角形(B)矩形(C)平行四边形(D)等腰梯形(3)矩形、菱形、正方形都具有的性质是()(A)对角线相等(B)对角线互相平分(C)对角线平分一组对角(D)对角线互相垂直CBBABDC八、典型举例:例1:如图,四边形ABCD为平行四边形,延长BA至E,延长DC至F,使BE=DF,AF交BC于H,CE交AD于G.求证:∠E=F∠ABHFCDEG分析:四边形ABCD是平行四边形ABCD∥=BE=DFAECF∥=四边形AFCE是平行四边形注:利用平行四边形的性质来证明线段或角相等是一种常用方法。∠E=F∠例2.已知:如图,矩形ABCD中,E是BC上一点,DFAE于F,若AE=BC,求证:CE=FE.ABCDEF分析:从求证入手,要证CE=FE,由已知AE=BC可知,只要证AF=BE即可,...