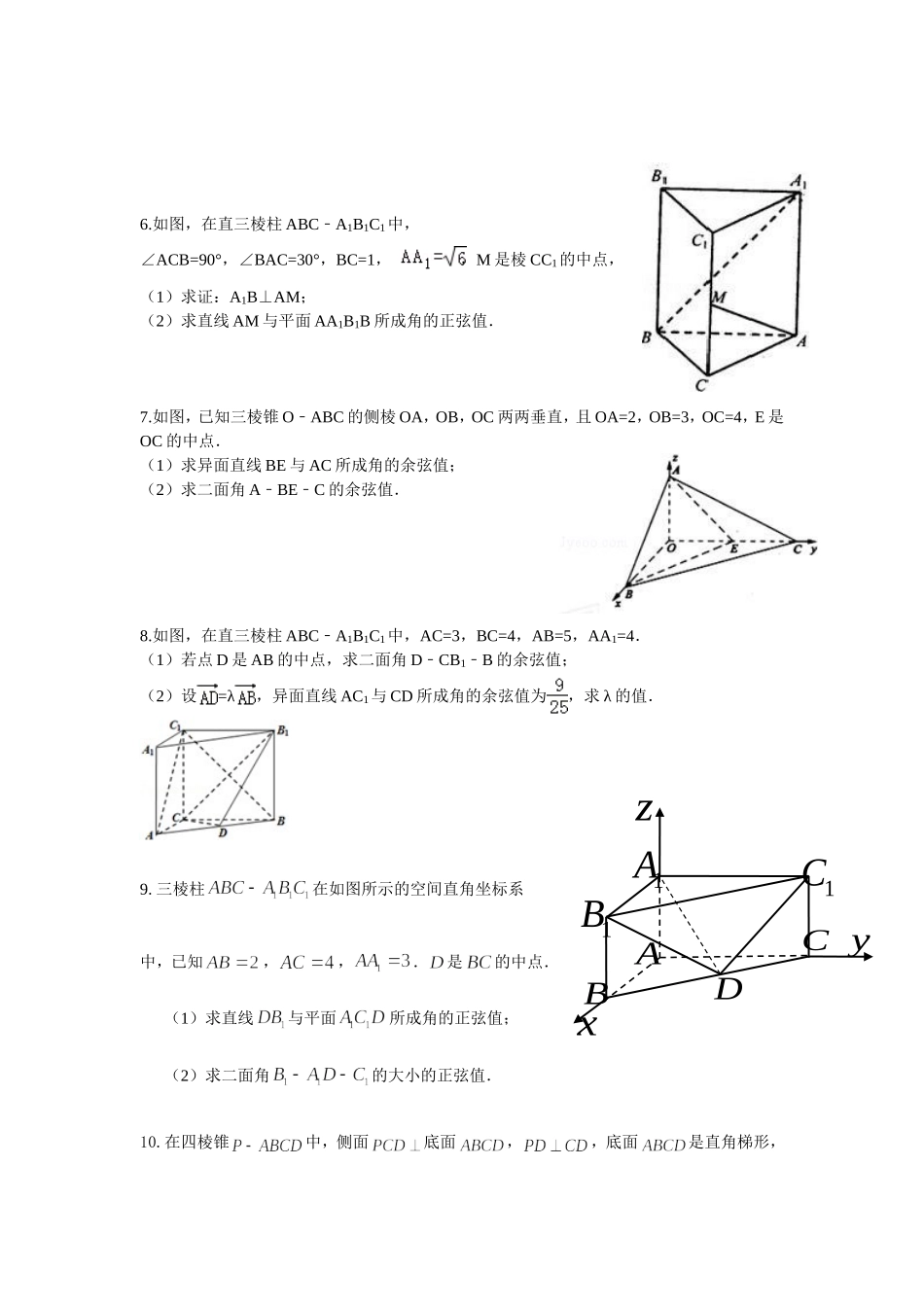
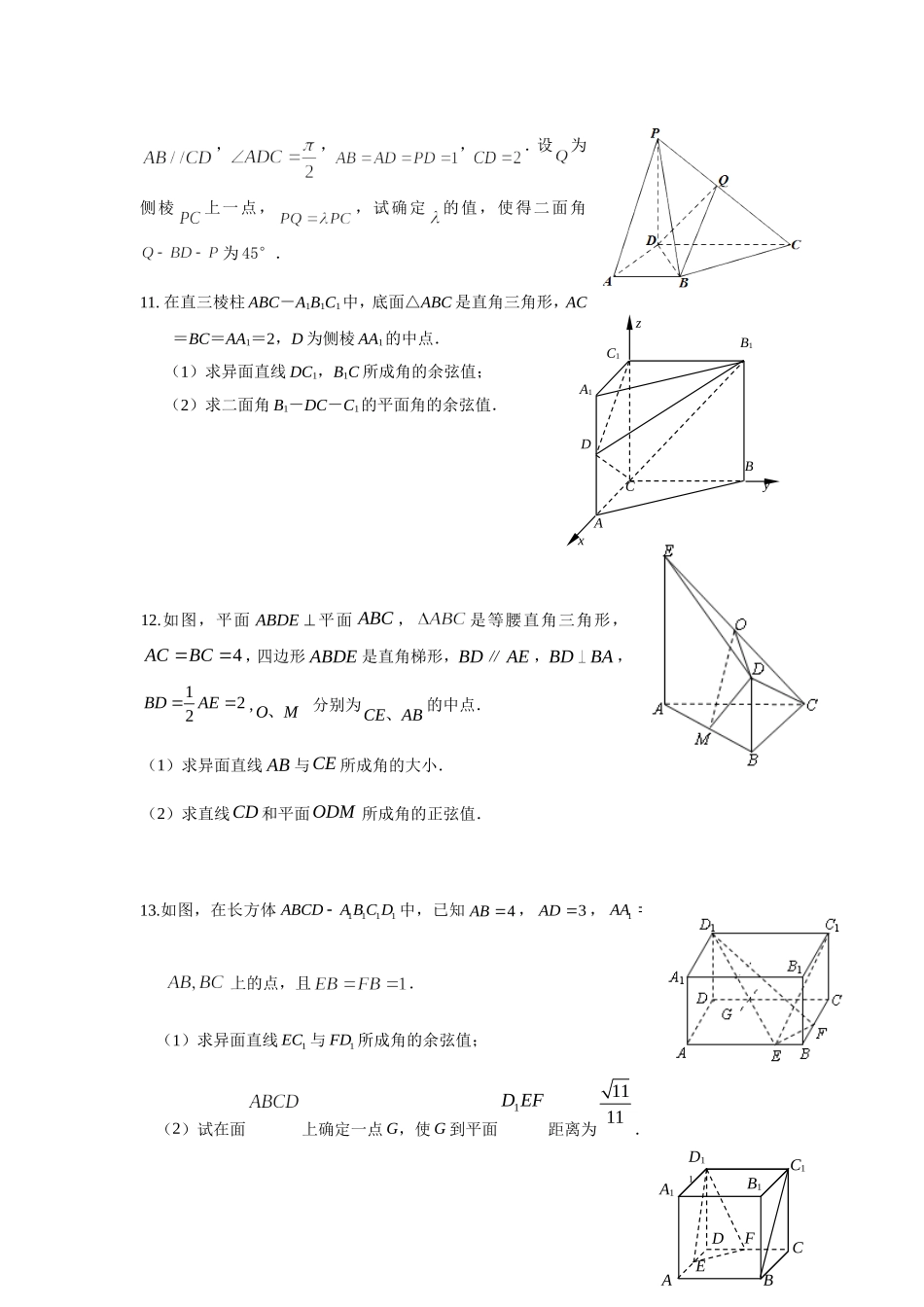
空间向量题库1.在正方体ABCD—A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且D1E=λEO(1)若λ=1,求异面直线DE与CD1所成的角的余弦值;(2)若平面CDE⊥平面CD1O,求λ的值。2.如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4.(1)设,异面直线AC1与CD所成角的余弦值为,求的值;(2)若点D是AB的中点,求二面角D-CB1-B的余弦值。3.如图所示,在棱长为2的正方体中,点分别在棱上,满足,且.(1)试确定、两点的位置.(2)求二面角大小的余弦值.4.如图,四边形ABCD是边长为1的正方形,MDABCD平面,NBABCD平面,且MD=NB=1,E为BC的中点(1)求异面直线NE与AM所成角的余弦值在线段AN上是否存在点S,使得ES平面AMN?若存在,求线段AS的长;若不存在,请说明理由5.如图,已知三棱柱的侧棱与底面垂直,,是的中点,是的中点,点在直线上,且满足.(1)当取何值时,直线与平面所成的角最大?(2)若平面与平面所成的二面角为,试确定点的位置.ADBCPA1B1C1QD1第22题1A1BPNMABC1C6.如图,在直三棱柱ABCA﹣1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,,M是棱CC1的中点,(1)求证:A1B⊥AM;(2)求直线AM与平面AA1B1B所成角的正弦值.7.如图,已知三棱锥OABC﹣的侧棱OA,OB,OC两两垂直,且OA=2,OB=3,OC=4,E是OC的中点.(1)求异面直线BE与AC所成角的余弦值;(2)求二面角ABEC﹣﹣的余弦值.8.如图,在直三棱柱ABCA﹣1B1C1中,AC=3,BC=4,AB=5,AA1=4.(1)若点D是AB的中点,求二面角DCB﹣1B﹣的余弦值;(2)设=λ,异面直线AC1与CD所成角的余弦值为,求λ的值.9.三棱柱在如图所示的空间直角坐标系中,已知,,.是的中点.(1)求直线与平面所成角的正弦值;(2)求二面角的大小的正弦值.10.在四棱锥中,侧面底面,,底面是直角梯形,1B1C1AyzBxACDABC1D11CDEFB1A1,,,.设为侧棱上一点,,试确定的值,使得二面角为45°.11.在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D为侧棱AA1的中点.(1)求异面直线DC1,B1C所成角的余弦值;(2)求二面角B1-DC-C1的平面角的余弦值.12.如图,平面ABDE平面ABC,是等腰直角三角形,4ACBC,四边形ABDE是直角梯形,BD∥AE,BDBA,122BDAE,OM、分别为CEAB、的中点.(1)求异面直线AB与CE所成角的大小.(2)求直线CD和平面ODM所成角的正弦值.13.如图,在长方体1111ABCDABCD中,已知4AB,3AD,12AA,分别是棱上的点,且.(1)求异面直线1EC与1FD所成角的余弦值;(2)试在面上确定一点G,使G到平面EFD1距离为1111.ABCA1B1C1DxzyPABCD1A1B1C1D(第22题图)14.(本小题满分10分)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为AD、DC的中点.(1)求直线BC1与平面EFD1所成角的正弦值;(2)设直线BC1上一点P满足平面PAC∥平面EFD1,求PB的长.15.如图,正四棱柱中,,,点在棱上,且.(I)求的长;(II)求钝角二面角的大小.16.如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.(Ⅰ)求证:AA1⊥平面ABC;(Ⅱ)求二面角A1-BC1-B1的余弦值;(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求的值.17.已知直三棱柱,底面是等腰三角形,,点分别是的中点.(Ⅰ)求证:直线平面;(Ⅱ)求直线与平面所成角的正弦值.18.如图,已知菱形的边长为,,.将菱形沿对角线折起,使,得到三棱锥.(Ⅰ)若点是棱的中点,求证:平面;(Ⅱ)求二面角的余弦值;(Ⅲ)设点是线段上一个动点,试确定点的位置,使得,并证明你的结论.20.如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点。(Ⅰ)求证:AE⊥PD;(Ⅱ)若直线PB与平面PAD所成角的正弦值为,求二面角E-AF-C的余弦值.21.如图,在四棱柱中,侧面⊥底面,,底面为直角梯形,其中,O为中点。(Ⅰ)求证:平面;(Ⅱ)求锐二面角A—C1D1—C的余弦值。22.如图,在三棱柱中,已知,侧面。(1)求直线与底面ABC所成角正切值;(2)在棱(不包含端点上确定一点的位置,使得(要求说明理由).(3)在(2)的条件下,若,求二面角的大小.23.如图,在四棱锥P—ABCD中,侧面PAD是...