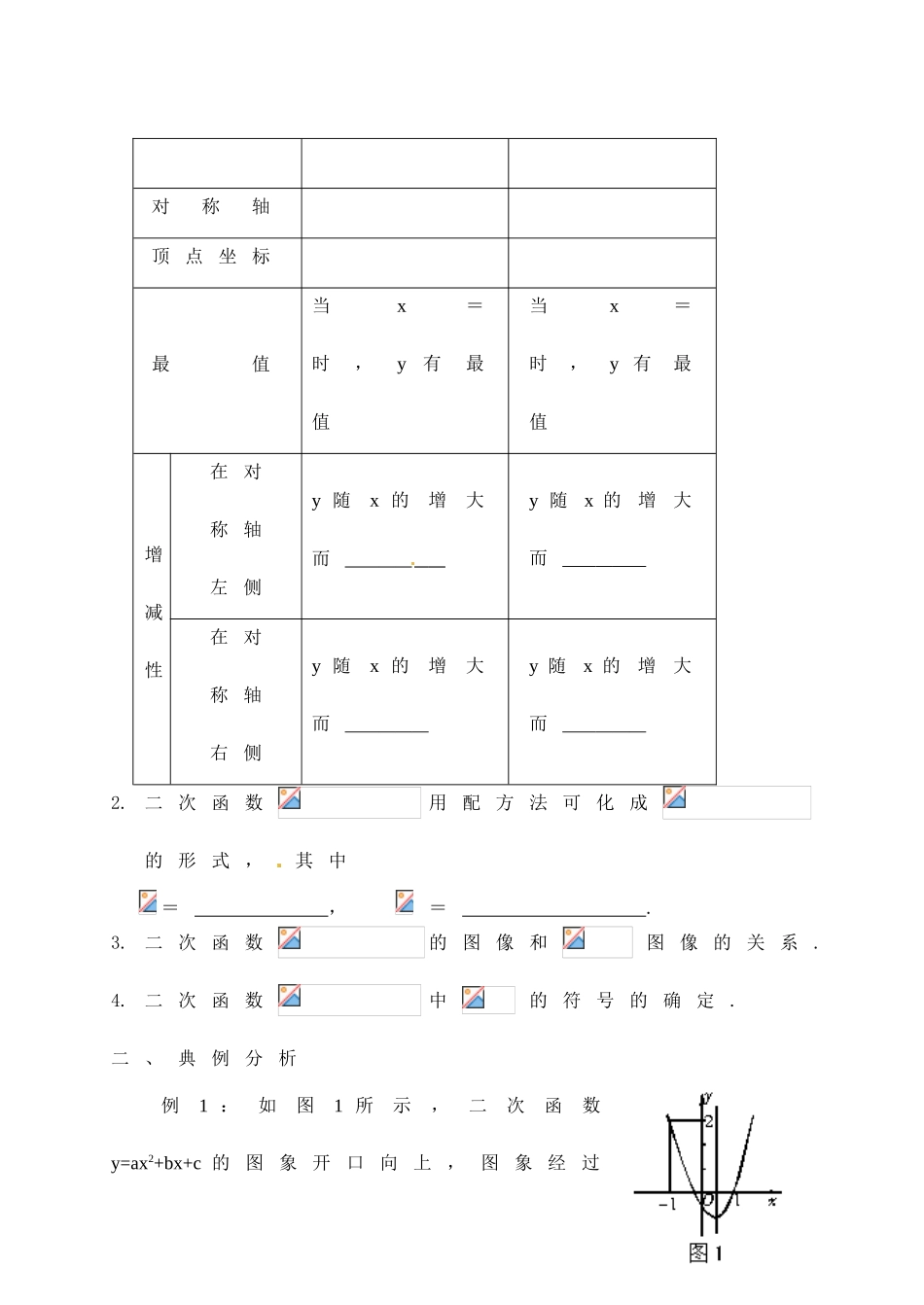
yxO第13课时二次函数图像与性质(一)班级姓名学号学习目标1.会利用对称性画出二次函数的图象,掌握二次函数的性质.2.会根据不同的条件,利用待定系数法求二次函数的函数关系式3.在实际应用中体会二次函数作为一种数学模型的作用,会利用二次函数的性质求实际问题中的最大或最小值.学习难点在实际应用中体会二次函数作为一种数学模型的作用,会利用二次函数的性质求实际问题教学过程一、考点链接1.二次函数的图像和性质>0<0图象开口对称轴顶点坐标最值当x=时,y有最值当x=时,y有最值增减性在对称轴左侧y随x的增大而y随x的增大而在对称轴右侧y随x的增大而y随x的增大而2.二次函数用配方法可化成的形式,其中=,=.3.二次函数的图像和图像的关系.4.二次函数中的符号的确定.二、典例分析例1:如图1所示,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0)且与y轴交于负半轴.第(1)问:给出四个结论:①a>0;②b>0;③c>0;④a+b+c=0,其中正确的结论的序号是.第(2)问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是_______.例2:抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点,(1)求出m的值并画出这条抛物线;(2)求它与x轴的交点和抛物线顶点的坐标;(3)x取什么值时,抛物线在x轴上方?(4)x取什么值时,y的值随x的增大而减小?三、巩固练习1.(2009年四川省内江市)抛物线的顶点坐标是()A.(2,3)B.(-2,3)C.(2,-3)D.(-2,-3)2.(2009年泸州)在平面直角坐标系中,将二次函数的图象向上平移2个单位,所得图象的解析式为()A.B.C.D.3.如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是()A.B.C.D.4.函数y=ax+1与y=ax2+bx+1(a≠0)的图象可能是()【课后作业】班级姓名学号1、(09长春)如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度大小不变,则以点A为圆心,线段AP长ABCD1111xoyyoxyoxxoy为半径的圆的面积S与点P的运动时间t之间的函数图象大致为()2、(09贵州)抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是()A、y=x2-x-2B、y=C、y=D、y=3、(09烟台)二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的图象大致为()4、(09天津)在平面直角坐标系中,先将抛物1OxyOStOStOStOStAPBA.B.C.D.(第8题)yxOyxOB.C.yxOA.yxOD.线关于轴作轴对称变换,再将所得的抛物线关于轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为()A.B.C.D.5、(09北京)若把代数式化为的形式,其中为常数,则=.6、(09安徽)已知二次函数的图象经过原点及点(,),且图象与x轴的另一交点到原点的距离为1,则该二次函数的解析式为7、(09鄂州)把抛物线y=ax+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x-3x+5,则a+b+c=__________8、(09兰州)二次函数的图象如图12所示,点位于坐标原点,点,,,…,在y轴的正半轴上,点,,,…,在二次函数位于第一象限的图象上,若△,△,△,…,△都为等边三角形,则△的边长=.9、(09重庆)如图,抛物线与x轴交与A(1,0),B(-3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.第9题图