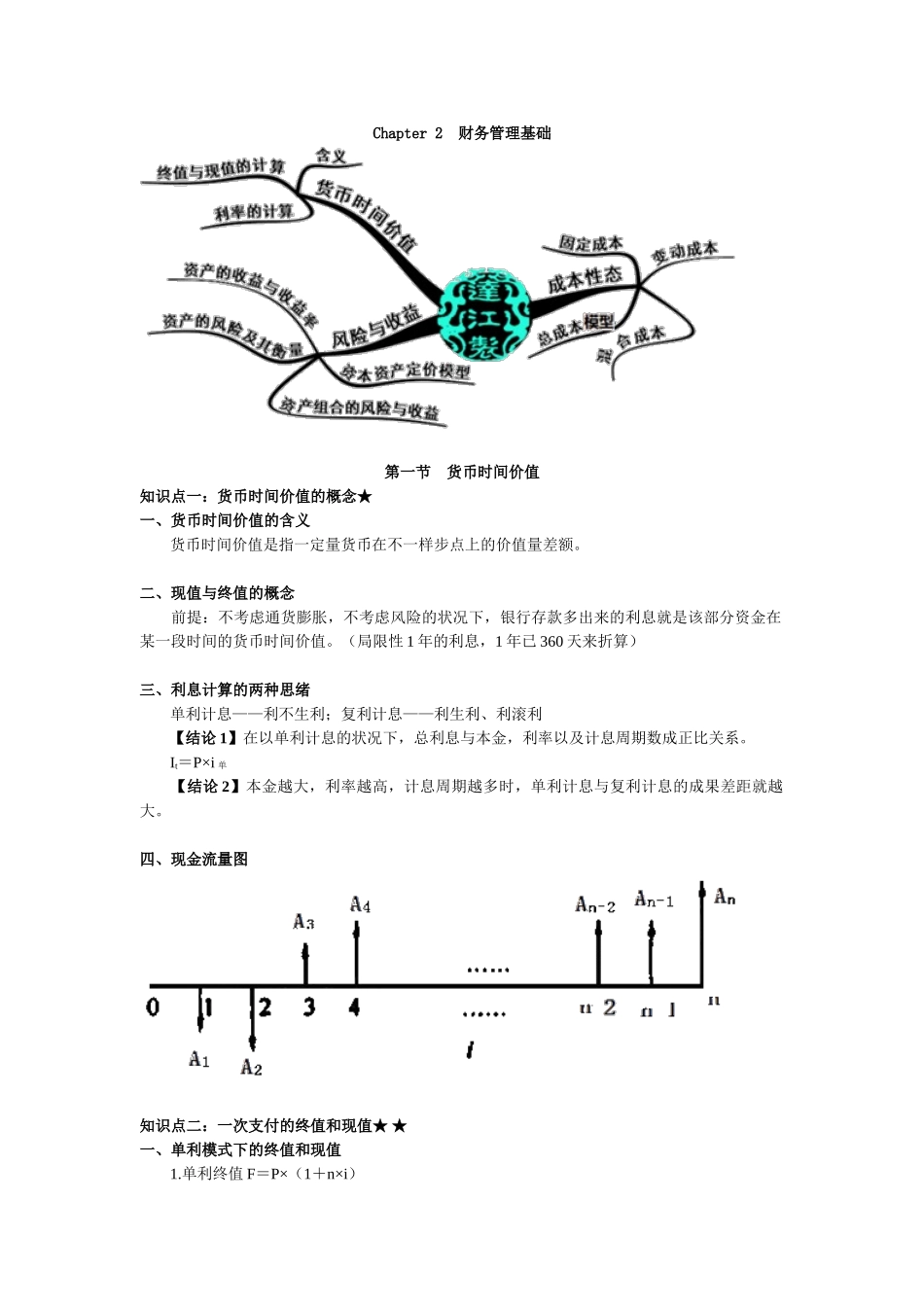
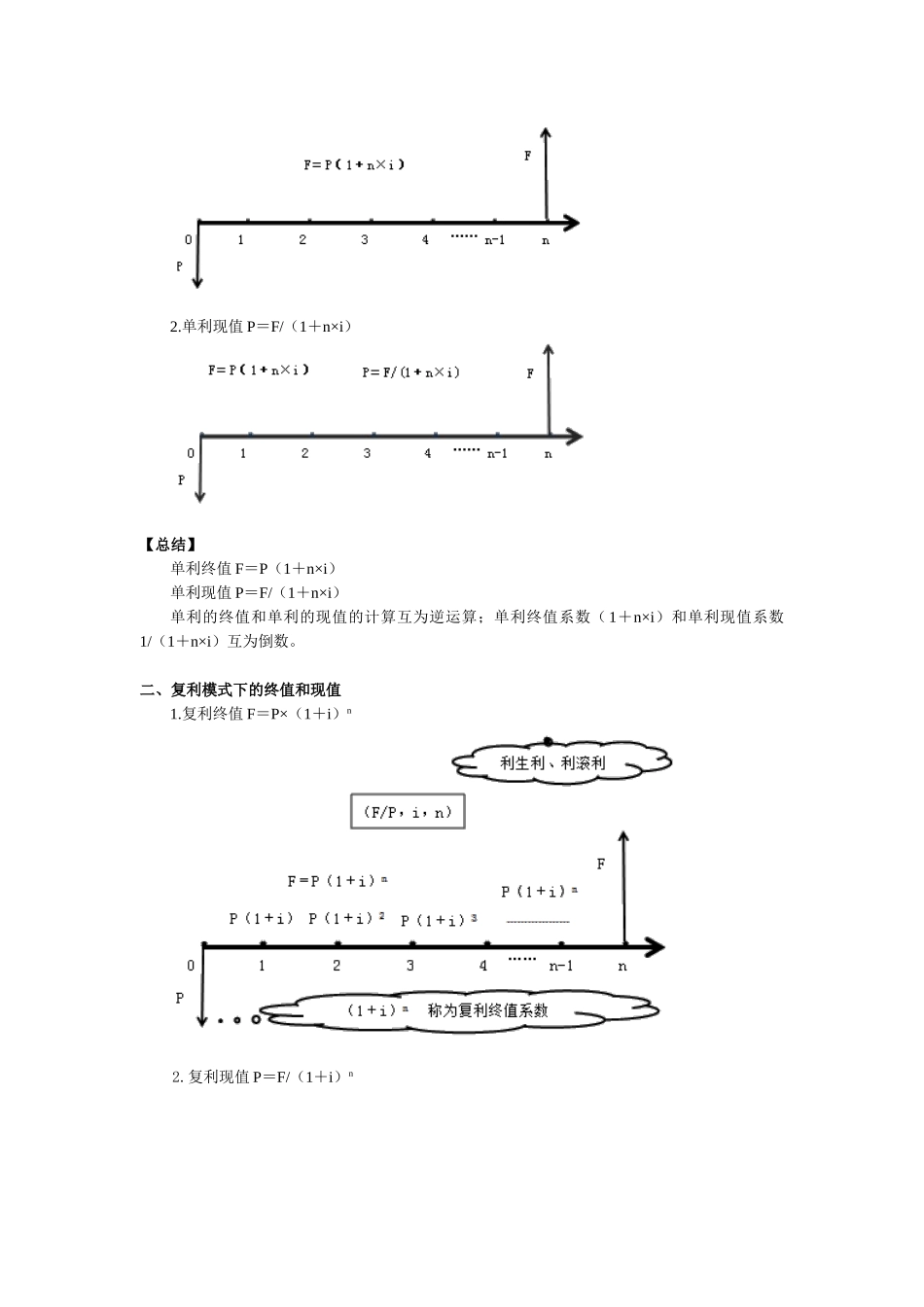
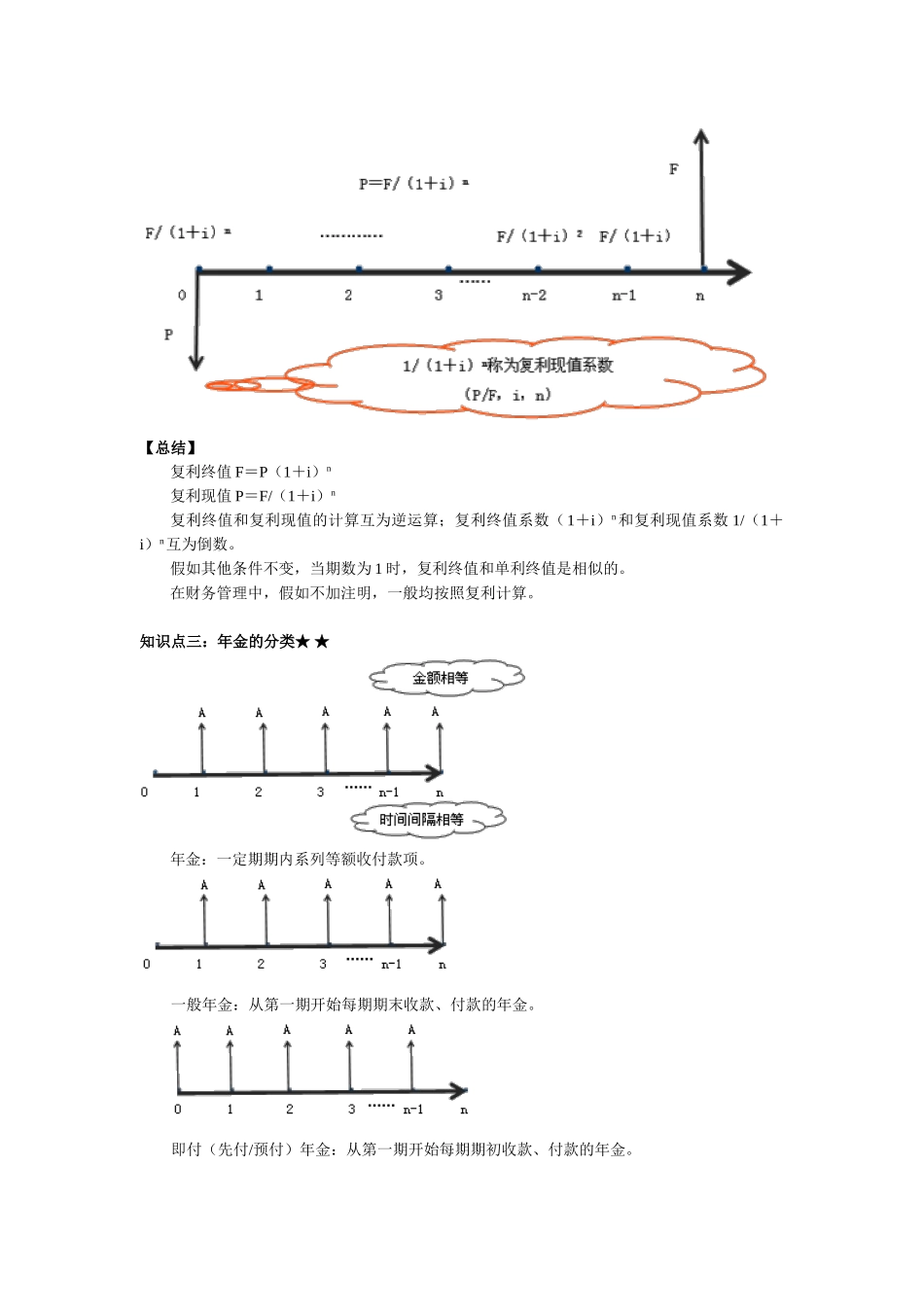
Chapter2财务管理基础第一节货币时间价值知识点一:货币时间价值的概念★一、货币时间价值的含义货币时间价值是指一定量货币在不一样步点上的价值量差额。二、现值与终值的概念前提:不考虑通货膨胀,不考虑风险的状况下,银行存款多出来的利息就是该部分资金在某一段时间的货币时间价值。(局限性1年的利息,1年已360天来折算)三、利息计算的两种思绪单利计息——利不生利;复利计息——利生利、利滚利【结论1】在以单利计息的状况下,总利息与本金,利率以及计息周期数成正比关系。It=P×i单【结论2】本金越大,利率越高,计息周期越多时,单利计息与复利计息的成果差距就越大。四、现金流量图知识点二:一次支付的终值和现值★★一、单利模式下的终值和现值1.单利终值F=P×(1+n×i)2.单利现值P=F/(1+n×i)【总结】单利终值F=P(1+n×i)单利现值P=F/(1+n×i)单利的终值和单利的现值的计算互为逆运算;单利终值系数(1+n×i)和单利现值系数1/(1+n×i)互为倒数。二、复利模式下的终值和现值1.复利终值F=P×(1+i)n2.复利现值P=F/(1+i)n【总结】复利终值F=P(1+i)n复利现值P=F/(1+i)n复利终值和复利现值的计算互为逆运算;复利终值系数(1+i)n和复利现值系数1/(1+i)n互为倒数。假如其他条件不变,当期数为1时,复利终值和单利终值是相似的。在财务管理中,假如不加注明,一般均按照复利计算。知识点三:年金的分类★★年金:一定期期内系列等额收付款项。一般年金:从第一期开始每期期末收款、付款的年金。即付(先付/预付)年金:从第一期开始每期期初收款、付款的年金。递延年金:在第二期或第二期后来收付的年金永续年金:无限期的一般年金知识点四:年金的终值和现值★★★一、年金终值(一)一般年金终值被称为年金终值系数,用符号(F/A,i,n)表达。(二)即付年金终值措施一:先求一般年金终值,再调整F=A(F/A,i,n)(1+i)措施二:先调时间差,再求一般年金终值F=A(F/A,i,n+1)-A=A[(F/A,i,n+1)-1](三)递延年金终值计算递延年金终值和计算一般年金终值基本同样,只是注意扣除递延期即可。第m+1期期初=第m期期末,递延期为m-1期F=A(F/A,i,n)二、年金现值(一)一般年金现值被称为年金现值系数,记作(P/A,i,n)。(二)预付年金现值措施一:先求一般年金现值,然后再调整P=A(P/A,i,n)(1+i)措施二:先调整时间差,然后求一般年金现值期终加一;期现减一P=A(P/A,i,n-1)+A=A[(P/A,i,n-1)+1](三)递延年金现值措施一:先求一般年金现值,然后折现P=A(P/A,i,n)×(P/F,i,m)措施二:假定一般年金模式,求现值后相减。P=A×(P/A,i,m+n)-A(P/A,i,m)措施三:先求已经有的年金终值,然后折现P=A×(F/A,i,n)×(P/F,i,m+n)4.永续年金现值P=A/i三、偿债基金F=A×(F/A,i,n)A=F/(F/A,i,n)1/(F/A,i,n)称为“偿债基金系数”,记作(A/F,i,n)。四、年资本回收额P=A×(P/A,i,n)A=P/(P/A,i,n)1/(P/A,i,n),称为资本回收系数,记作(A/P,i,n)。总结一般年金:F=A×(F/A,i,n)P=A×(P/A,i,n)即付年金:递延年金:F=A(F/A,i,n)P=A×(P/A,i,n)×(P/F,i,m)P=A×(P/A,i,m+n)-A(P/A,i,m)P=A×(F/A,i,n)×(P/F,i,m+n)永续年金:P=A/i知识点五:利率的计算★★★一、复利计息方式下的利率计算思绪:已知现值(或终值)系数,可通过内插法计算对应的利率(不要记忆该公式,需要做题来理解原理)二、名义利率与实际利率(一)一年多次计息时的名义利率与实际利率名义利率:假如以“年”作为基本计息期,每年计算一次复利,此时的年利率为名义利率(r);实际利率:假如按照短于1年的计息期计算复利,并将整年利息额除以年初的本金,此时得到的利率为实际利率(i)。i=利息/本金=(终值-现值)/现值=(F-P)/P=[(P×(1+r/m)m-P]/Pi=(1+r/m)m-1(二)通货膨胀状况下的名义利率与实际利率通货膨胀状况下的名义利率,包括赔偿通货膨胀(包括通货紧缩)风险的利...