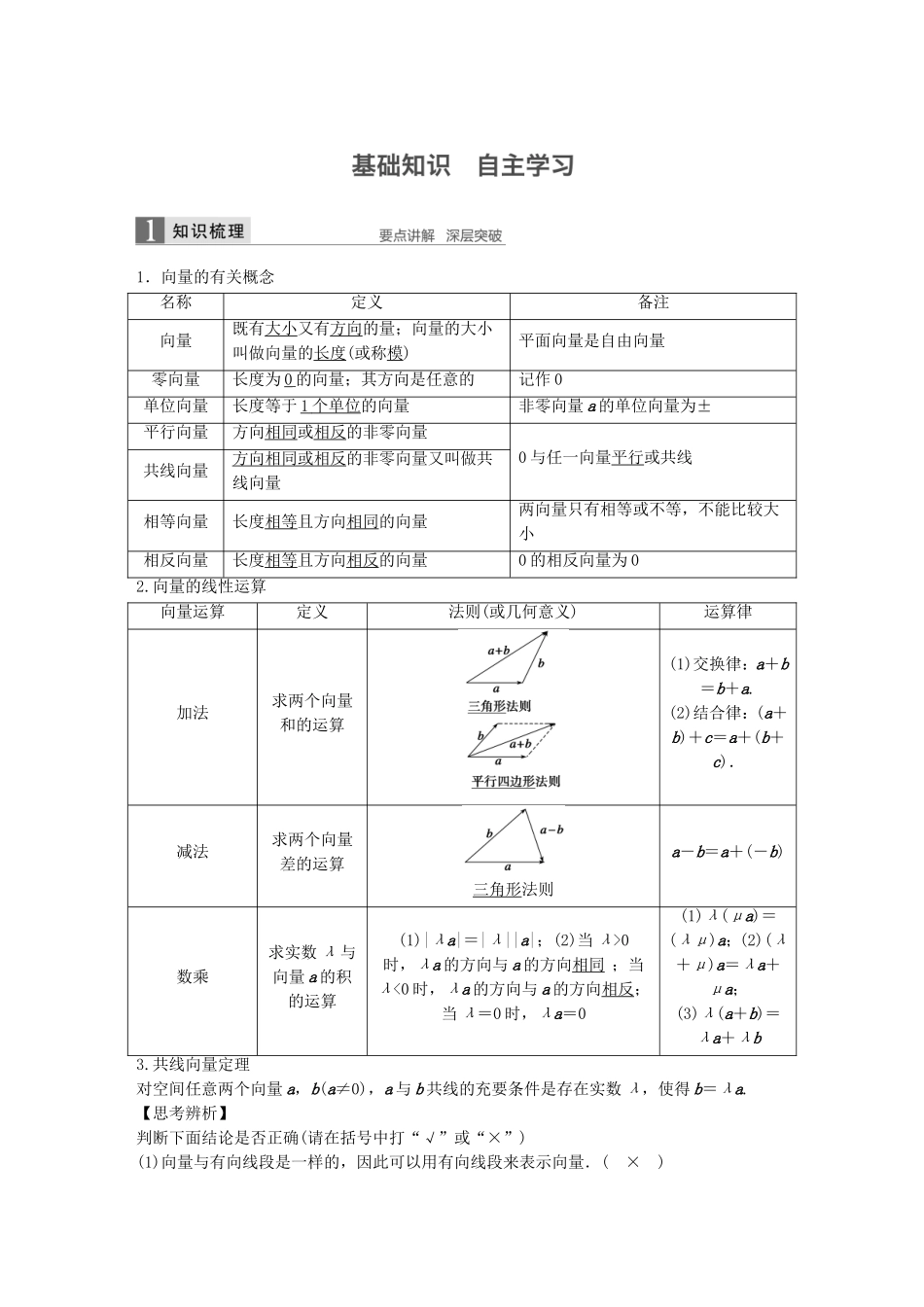
1.向量的有关概念名称定义备注向量既有大小又有方向的量;向量的大小叫做向量的长度(或称模)平面向量是自由向量零向量长度为0的向量;其方向是任意的记作0单位向量长度等于1个单位的向量非零向量a的单位向量为±平行向量方向相同或相反的非零向量0与任一向量平行或共线共线向量方向相同或相反的非零向量又叫做共线向量相等向量长度相等且方向相同的向量两向量只有相等或不等,不能比较大小相反向量长度相等且方向相反的向量0的相反向量为02.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律:a+b=b+a.(2)结合律:(a+b)+c=a+(b+c).减法求两个向量差的运算三角形法则a-b=a+(-b)数乘求实数λ与向量a的积的运算(1)|λa|=|λ||a|;(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa=0(1)λ(μa)=(λμ)a;(2)(λ+μ)a=λa+μa;(3)λ(a+b)=λa+λb3.共线向量定理对空间任意两个向量a,b(a≠0),a与b共线的充要条件是存在实数λ,使得b=λa.【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)向量与有向线段是一样的,因此可以用有向线段来表示向量.(×)(2)|a|与|b|是否相等与a,b的方向无关.(√)(3)若a∥b,b∥c,则a∥c.(×)(4)向量AB与向量CD是共线向量,则A,B,C,D四点在一条直线上.(×)(5)当两个非零向量a,b共线时,一定有b=λa,反之成立.(√)(6)△ABC中,D是BC中点,则AD=(AC+AB).(√)1.给出下列命题:①零向量的长度为零,方向是任意的;②若a,b都是单位向量,则a=b;③向量AB与BA相等.则所有正确命题的序号是________.答案①解析根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量AB与BA互为相反向量,故③错误.2.如图所示,向量a-b=________(用e1,e2表示).答案e1-3e2解析由题图可得a-b=BA=e1-3e2.3.设D为△ABC所在平面内一点,BC=3CD,则AD=______________(用AB,AC表示).答案-AB+AC解析 BC=3CD,∴AC-AB=3(AD-AC),即4AC-AB=3AD,∴AD=-AB+AC.4.已知▱ABCD的对角线AC和BD相交于O,且OA=a,OB=b,则DC=________,BC=________(用a,b表示).答案b-a-a-b解析如图,DC=AB=OB-OA=b-a,BC=OC-OB=-OA-OB=-a-b.5.已知a与b是两个不共线向量,且向量a+λb与-(b-3a)共线,则λ=________.答案-解析由已知得a+λb=-k(b-3a),∴解得题型一平面向量的概念例1下列命题中,正确的是________.(填序号)①有向线段就是向量,向量就是有向线段;②向量a与向量b平行,则a与b的方向相同或相反;③向量AB与向量CD共线,则A、B、C、D四点共线;④两个向量不能比较大小,但它们的模能比较大小.答案④解析①不正确,向量可以用有向线段表示,但向量不是有向线段,有向线段也不是向量;②不正确,若a与b中有一个为零向量,零向量的方向是不确定的,故两向量方向不一定相同或相反;③不正确,共线向量所在的直线可以重合,也可以平行;④正确,向量既有大小,又有方向,不能比较大小;向量的模均为实数,可以比较大小.思维升华(1)相等向量具有传递性,非零向量的平行也具有传递性.(2)共线向量即为平行向量,它们均与起点无关.(3)向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象的移动混为一谈.(4)非零向量a与的关系:是与a同方向的单位向量.设a0为单位向量,①若a为平面内的某个向量,则a=|a|a0;②若a与a0平行,则a=|a|a0;③若a与a0平行且|a|=1,则a=a0.上述命题中,假命题的个数是________.答案3解析向量是既有大小又有方向的量,a与|a|a0的模相同,但方向不一定相同,故①是假命题;若a与a0平行,则a与a0的方向有两种情况:一是同向,二是反向,反向时a=-|a|a0,故②③也是假命题.综上所述,假命题的个数是3.题型二平面向量的线性运算命题点1向量的线性运算例2(1)设D,E,F分别为△ABC的三边BC,CA,AB的中点,则EB+FC=________.(2)在△ABC中,AB=c,AC=b,若点D满足BD=...