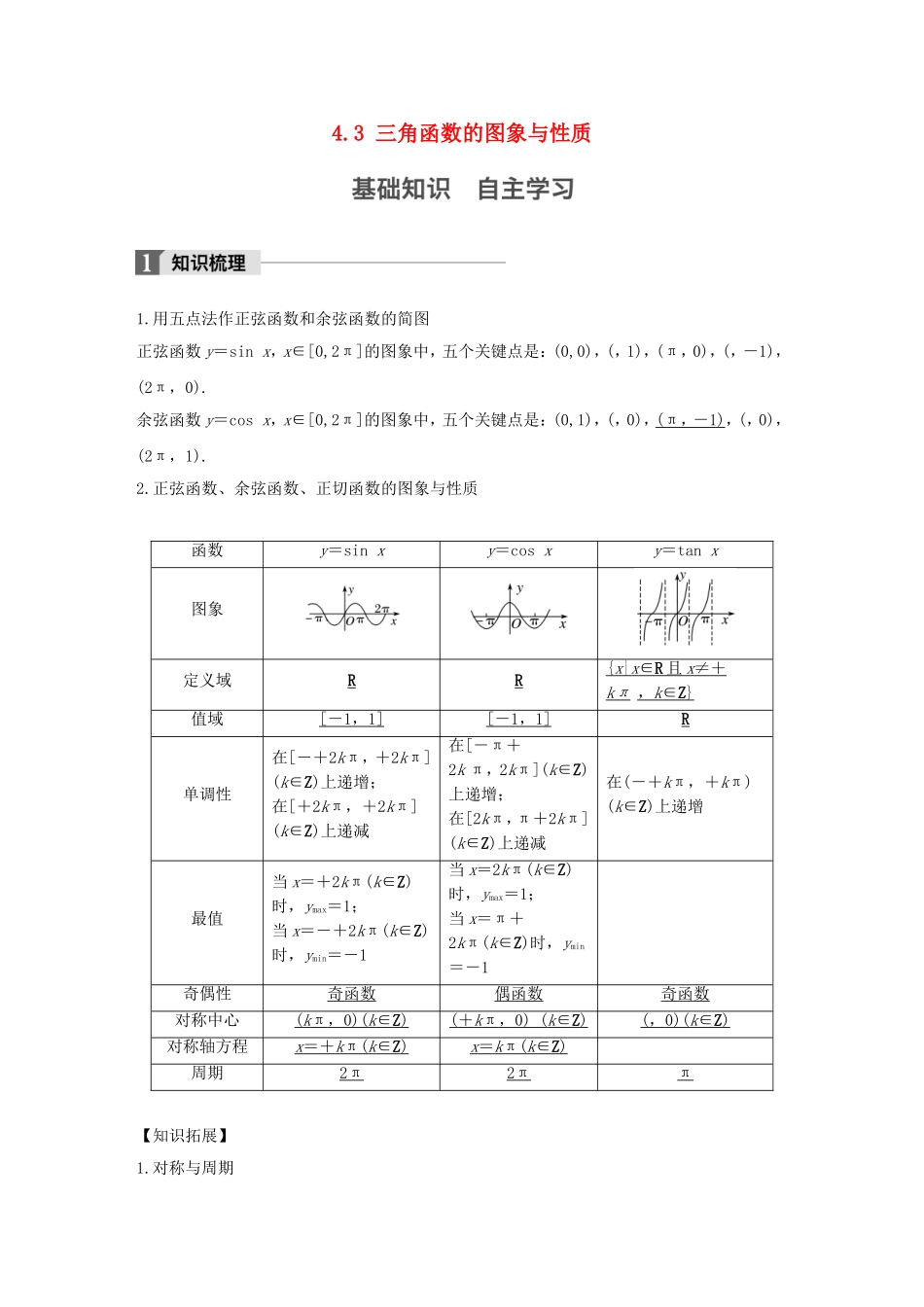
4.3三角函数的图象与性质1.用五点法作正弦函数和余弦函数的简图正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0),(,1),(π,0),(,-1),(2π,0).余弦函数y=cosx,x∈[0,2π]的图象中,五个关键点是:(0,1),(,0),(π,-1),(,0),(2π,1).2.正弦函数、余弦函数、正切函数的图象与性质函数y=sinxy=cosxy=tanx图象定义域RR{x|x∈R且x≠+kπ,k∈Z}值域[-1,1][-1,1]R单调性在[-+2kπ,+2kπ](k∈Z)上递增;在[+2kπ,+2kπ](k∈Z)上递减在[-π+2kπ,2kπ](k∈Z)上递增;在[2kπ,π+2kπ](k∈Z)上递减在(-+kπ,+kπ)(k∈Z)上递增最值当x=+2kπ(k∈Z)时,ymax=1;当x=-+2kπ(k∈Z)时,ymin=-1当x=2kπ(k∈Z)时,ymax=1;当x=π+2kπ(k∈Z)时,ymin=-1奇偶性奇函数偶函数奇函数对称中心(kπ,0)(k∈Z)(+kπ,0)(k∈Z)(,0)(k∈Z)对称轴方程x=+kπ(k∈Z)x=kπ(k∈Z)周期2π2ππ【知识拓展】1.对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是个周期.(2)正切曲线相邻两对称中心之间的距离是半个周期.2.奇偶性若f(x)=Asin(ωx+φ)(A,ω≠0),则(1)f(x)为偶函数的充要条件是φ=+kπ(k∈Z);(2)f(x)为奇函数的充要条件是φ=kπ(k∈Z).【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”)(1)y=sinx在第一、第四象限是增函数.(×)(2)常数函数f(x)=a是周期函数,它没有最小正周期.(√)(3)正切函数y=tanx在定义域内是增函数.(×)(4)已知y=ksinx+1,x∈R,则y的最大值为k+1.(×)(5)y=sin|x|是偶函数.(√)(6)若sinx>,则x>.(×)1.函数f(x)=cos(2x-)的最小正周期是________.答案π解析最小正周期为T===π.2.(教材改编)函数y=-tanx的单调递减区间是________________.答案(-+kπ,+kπ)(k∈Z)解析因为y=tanx与y=-tanx的单调性相反,所以y=-tanx的单调递减区间为(-+kπ,+kπ)(k∈Z).3.(教材改编)sin11°,cos10°,sin168°的大小关系为________________.答案sin11°<sin168°<cos10°解析sin168°=sin(180°-12°)=sin12°,cos10°=sin(90°-10°)=sin80°,又y=sinx在[0°,90°]上是增函数,∴sin11°<sin12°<sin80°,即sin11°<sin168°<cos10°.4.(教材改编)y=1+sinx,x∈[0,2π]的图象与直线y=的交点个数为________.答案2解析在同一坐标系中作出函数y=1+sinx,x∈[0,2π]和y=的图象(图略),由图象可得有两个交点.5.(教材改编)下列满足函数y=tan的条件是________.(填序号)①在(0,)上单调递增;②为奇函数;③以π为最小正周期;④定义域为{x|x≠+,k∈Z}.答案①②解析①令0