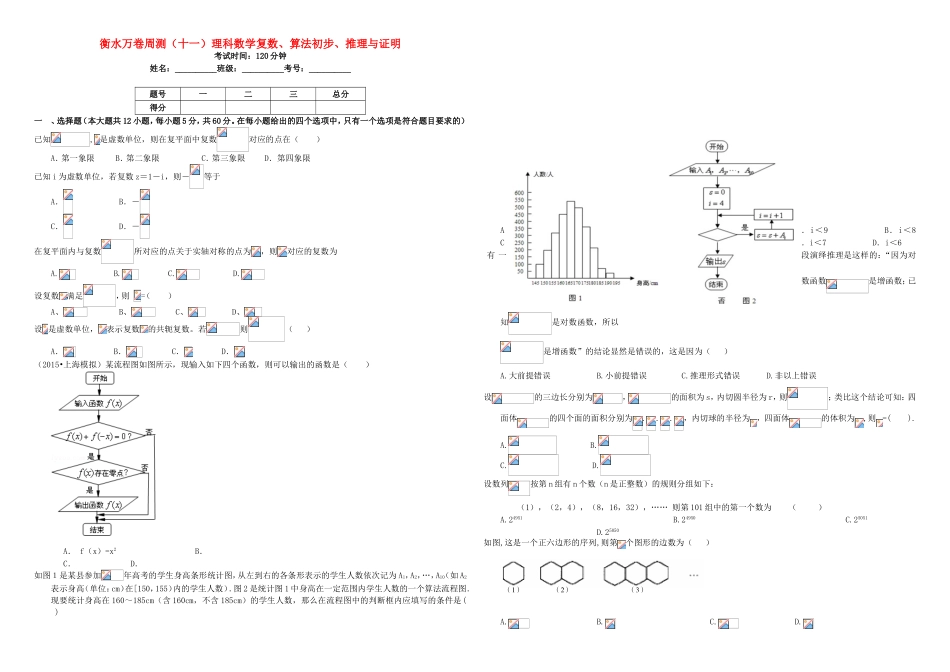
衡水万卷周测(十一)理科数学复数、算法初步、推理与证明考试时间:120分钟姓名:__________班级:__________考号:__________题号一二三总分得分一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)已知,是虚数单位,则在复平面中复数对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限已知i为虚数单位,若复数z=1-i,则-等于A.B.-C.D.-在复平面内与复数所对应的点关于实轴对称的点为,则对应的复数为A.B.C.D.设复数满足,则=()A、B、C、D、设是虚数单位,表示复数的共轭复数。若则()A.B.C.D.(2015•上海模拟)某流程图如图所示,现输入如下四个函数,则可以输出的函数是()A.f(x)=x2B.C.D.如图1是某县参加年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A1,A2,…,A10(如A2表示身高(单位:cm)在[150,155)内的学生人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~185cm(含160cm,不含185cm)的学生人数,那么在流程图中的判断框内应填写的条件是()A.i<9B.i<8C.i<7D.i<6有一段演绎推理是这样的:“因为对数函数是增函数;已知是对数函数,所以是增函数”的结论显然是错误的,这是因为()A.大前提错误B.小前提错误C.推理形式错误D.非以上错误设的三边长分别为,的面积为s,内切圆半径为r,则;类比这个结论可知:四面体的四个面的面积分别为...,内切球的半径为,四面体的体积为,则=().A.B.C.D.设数列按第n组有n个数(n是正整数)的规则分组如下:(1),(2,4),(8,16,32),……则第101组中的第一个数为()A.24951B.24950C.25051D.25050如图,这是一个正六边形的序列,则第个图形的边数为()(1)(2)(3)A.B.C.D.已知结论:“在正三角形中,若的边的中点,是三角形的重心,则”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体中,若的中心为,四面体内部一点到四面体各面的距离都相等”,则A.1B.2C.3D.4二、填空题(本大题共4小题,每小题5分,共20分)观察下列等式:…照此规律,第n个等式可为.观察下列算式,猜测由此表提供的一般法则,用适当的数学式子表示它。1=1,3+5=8,7+9+11=27,13+15+17+19=64,21+23+25+27+29=125,则这个式子为。有下列各式:,,,……则按此规律可猜想此类不等式的一般形式为:.设函数,观察:;;;.根据以上的事实,由归纳推理可得:当且时,=三、解答题(本大题共6小题,第1题10分,后5题每题12分,共70分)实数分别取什么值时,复数对应的点在(1)第三象限;(2)第四象限;(3)在直线上。已知集合,,,令表示集合所含元素的个数.(1)写出的值;(2)当时,写出的表达式,并用数学归纳法证明.先阅读下列不等式的证法,再解决后面的问题:已知求证.证明函数:构造函数,则.因为对一切,恒有,所以所以.(1)若,请写出上述结论的推广式;(2)类比上述证法,对你推广的结论加以证明.设实数,整数,。(I)证明:当且时,;(II)数列满足,,证明:。设是由个实数组成的行列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”。123101(1)数表如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1123-7-2101(2)数表如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数的所有可能值;表2a-a2-aa-2(3)对由个实数组成的行列的任意一个数表,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由。已知数列中,(1)设,求数列的通项公式;(2)求使不等式成立的的取值范围。衡水万卷周测(十一)答案解析一、选择题ADB【解析】==1+i,∴复数的共轭复数是1-i,就是复数,所对应的点关于实轴对称的点为A对应的复数;【思路点拨】用两个复数代数形式的乘除法法则,化简复数得到复数的共轭复数,...