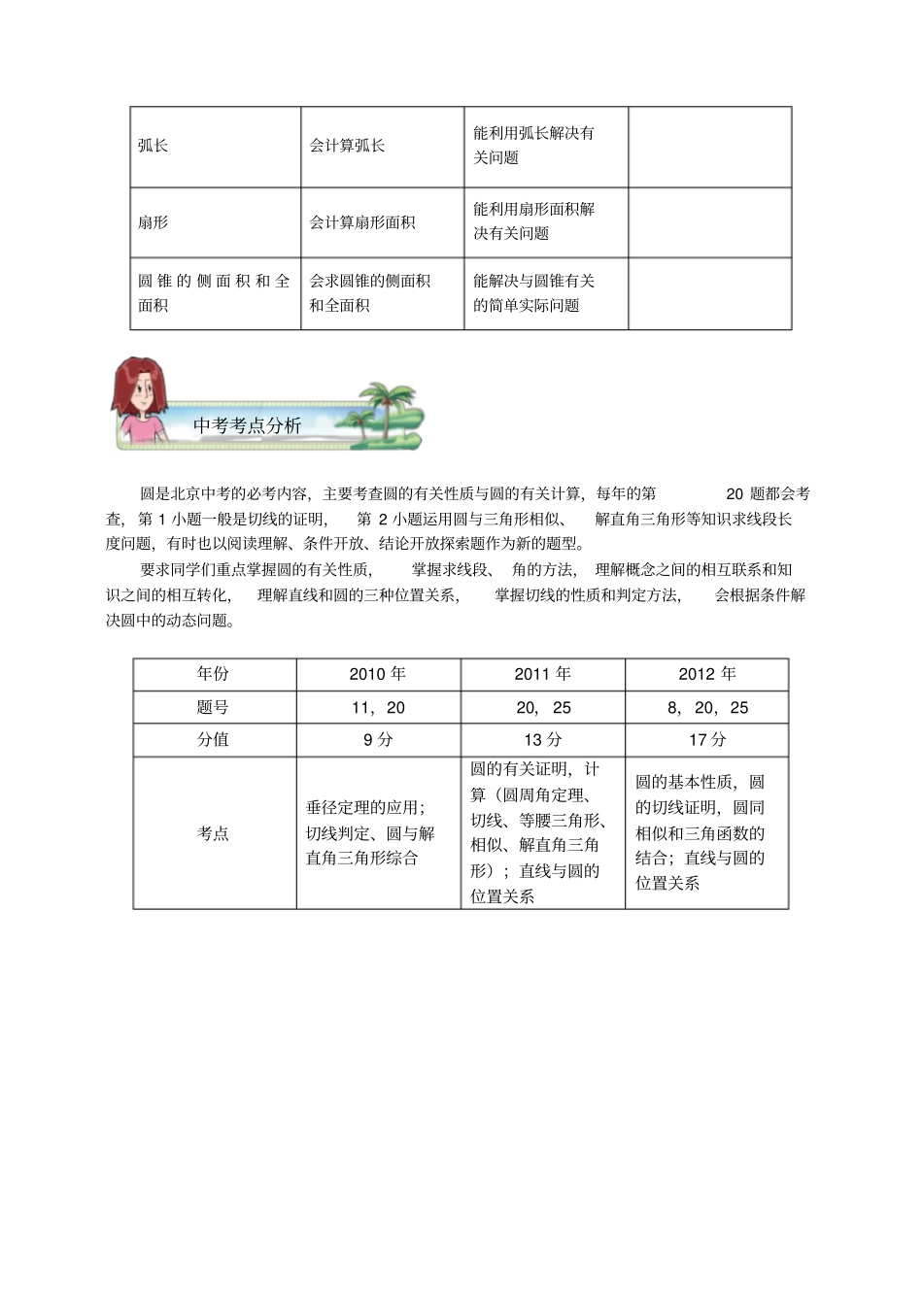
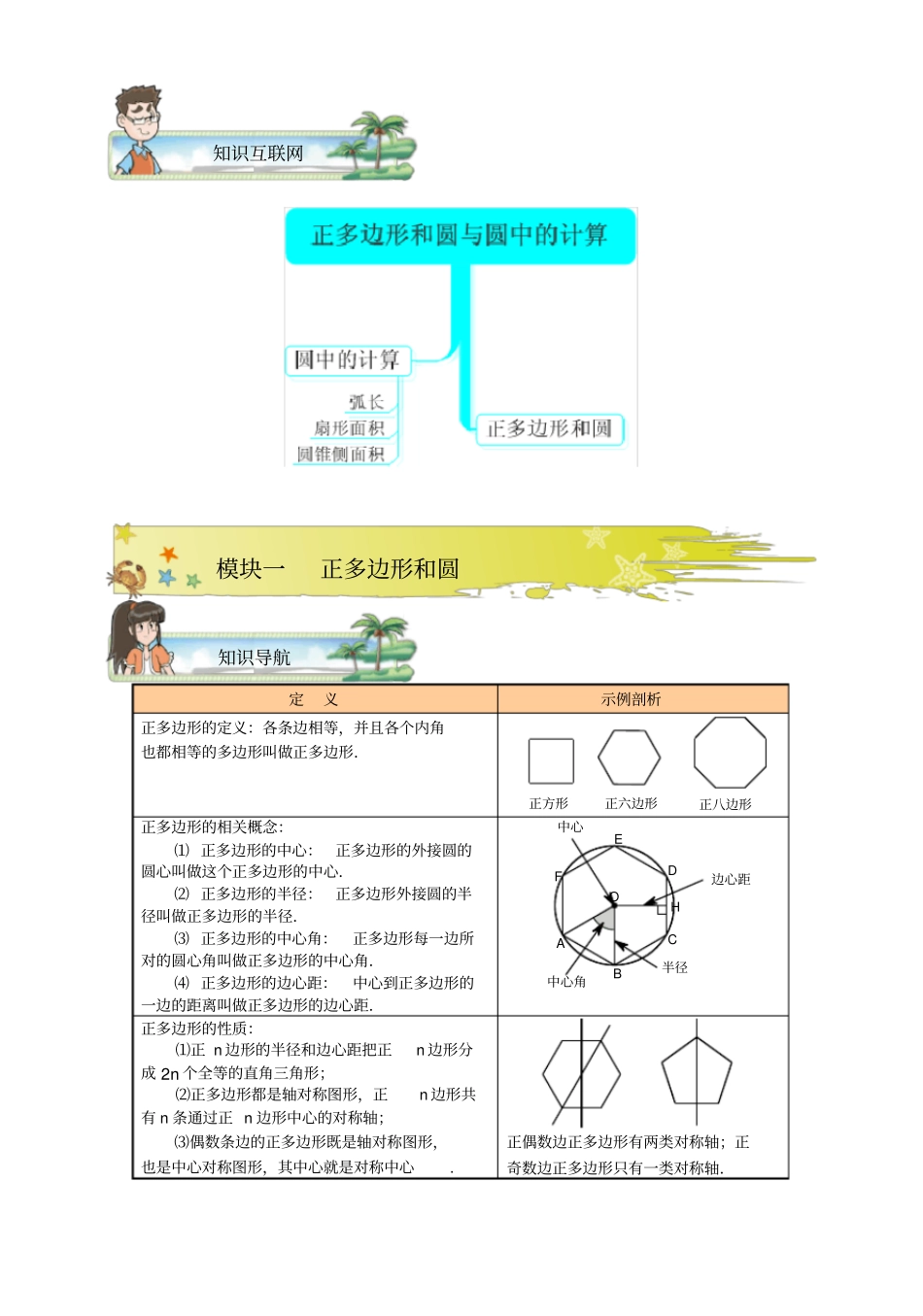
中考内容中考要求ABC圆的有关概念理解圆及其有关概念会过不在同一直线上的三点作圆;能利用圆的有关概念解决简单问题圆的性质知道圆的对称性,了解弧、弦、圆心角的关系能用弧、弦、圆心角的关系解决简单问题能运用圆的性质解决有关问题圆周角了解圆周角与圆心角的关系;知道直径所对的圆周角是直角会求圆周角的度数,能用圆周角的知识解决与角有关的简单问题能综合运用几何知识解决与圆周角有关的问题垂径定理会在相应的图形中确定垂径定理的条件和结论能用垂径定理解决有关问题点与圆的位置关系了解点与圆的位置关系直线与圆的位置关系了解直线与圆的位置关系;了解切线的概念,理解切线与过切点的半径之间的关系;会过圆上一点画圆的切线;了解切线长的概念能判定直线和圆的位置关系;会根据切线长的知识解决简单的问题;能利用直线和圆的位置关系解决简单问题能解决与切线有关的问题圆与圆的位置关系了解圆与圆的位置关系能利用圆与圆的位置关系解决简单问题中考内容与要求正多边形和圆与圆中的计算弧长会计算弧长能利用弧长解决有关问题扇形会计算扇形面积能利用扇形面积解决有关问题圆锥的侧面积和全面积会求圆锥的侧面积和全面积能解决与圆锥有关的简单实际问题圆是北京中考的必考内容,主要考查圆的有关性质与圆的有关计算,每年的第20题都会考查,第1小题一般是切线的证明,第2小题运用圆与三角形相似、解直角三角形等知识求线段长度问题,有时也以阅读理解、条件开放、结论开放探索题作为新的题型。要求同学们重点掌握圆的有关性质,掌握求线段、角的方法,理解概念之间的相互联系和知识之间的相互转化,理解直线和圆的三种位置关系,掌握切线的性质和判定方法,会根据条件解决圆中的动态问题。年份2010年2011年2012年题号11,2020,258,20,25分值9分13分17分考点垂径定理的应用;切线判定、圆与解直角三角形综合圆的有关证明,计算(圆周角定理、切线、等腰三角形、相似、解直角三角形);直线与圆的位置关系圆的基本性质,圆的切线证明,圆同相似和三角函数的结合;直线与圆的位置关系中考考点分析定义示例剖析正多边形的定义:各条边相等,并且各个内角也都相等的多边形叫做正多边形.正方形正六边形正八边形正多边形的相关概念:⑴正多边形的中心:正多边形的外接圆的圆心叫做这个正多边形的中心.⑵正多边形的半径:正多边形外接圆的半径叫做正多边形的半径.⑶正多边形的中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.⑷正多边形的边心距:中心到正多边形的一边的距离叫做正多边形的边心距.HOFEDCBA边心距中心角半径中心正多边形的性质:⑴正n边形的半径和边心距把正n边形分成2n个全等的直角三角形;⑵正多边形都是轴对称图形,正n边形共有n条通过正n边形中心的对称轴;⑶偶数条边的正多边形既是轴对称图形,也是中心对称图形,其中心就是对称中心.正偶数边正多边形有两类对称轴;正奇数边正多边形只有一类对称轴.知识互联网模块一正多边形和圆知识导航T2T1O【例1】⑴小亮从A点出发前进10m,向右转15,再前进10m,又向右转15⋯⋯这样一直走下去,他第一次回到出发点A时,一共走了_________m.⑵如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为()A.23B.323C.232D.3232(2012咸宁)⑶正八边形的一个内角等于_________,它的中心角等于___________.⑷若正ABC△外接圆的半径为R,则ABC△的面积为_____________.⑸半径为2cm的圆内接正方形的对角线长为__________cm,面积为____________2cm.⑹正六边形的边长为a,半径为R,边心距r的比::aRr__________________.(西城区教研)【解析】⑴240;⑵A;⑶135,45;⑷2334R;⑸4,8;⑹2:2:3.【例2】如图,有一个圆O和两个正六边形12TT,.1T的6个顶点都在圆周上,2T的6条边都和圆O相切(我们称12TT,分别为圆O的内接正六边形和外切正六边形).⑴设12TT,的边长分别为ab,,圆O的半径为r,求:ra及:rb的值;⑵求正六边形12TT,的面积比12:SS的值.【解析】⑴3:1:2rarb,;⑵222212333333664242SaaSbb,由⑴:3:2ab,∴22123::4SSab.能力提升夯实基础模块二圆中的计算15°15°AFABOCDE...