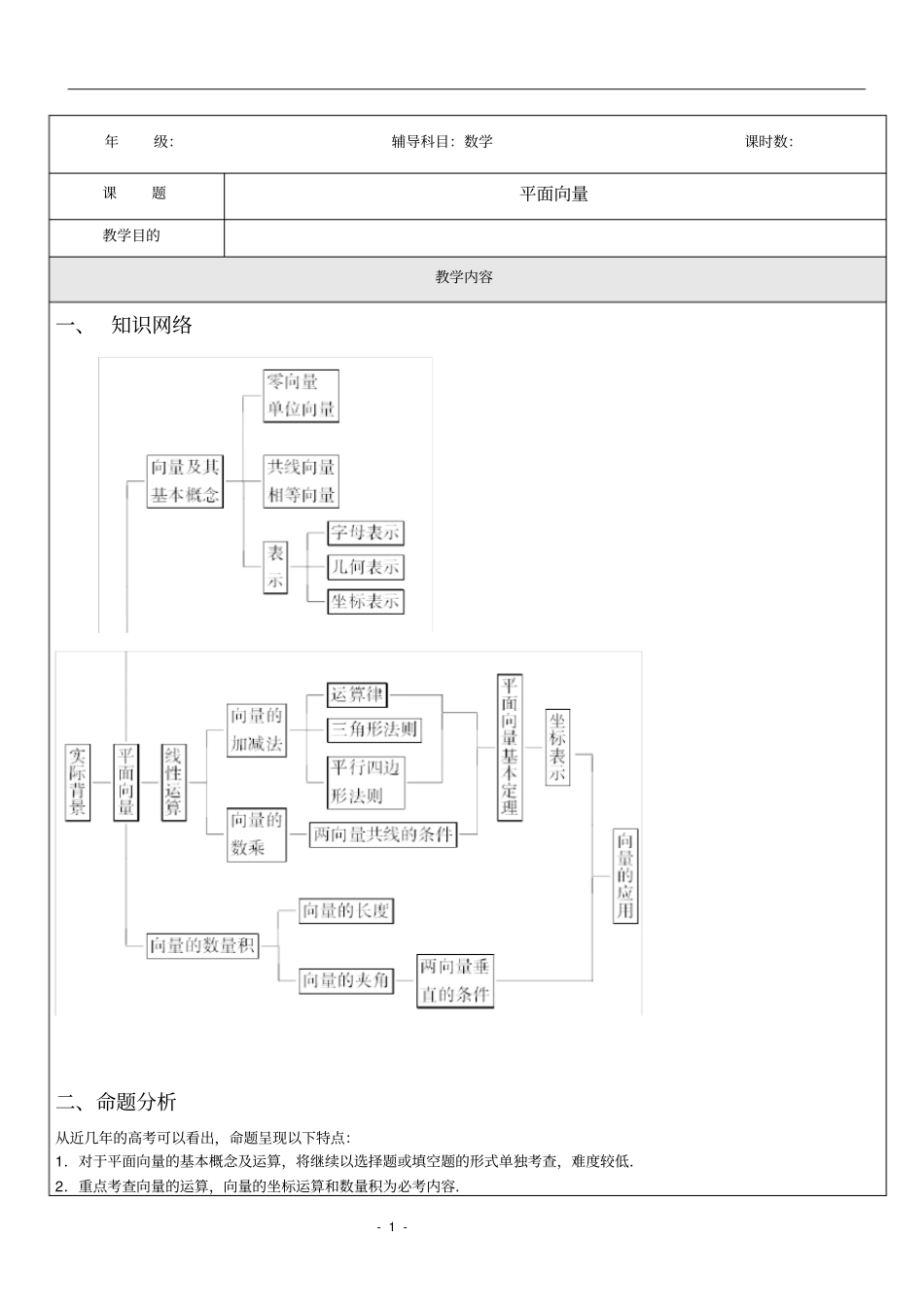
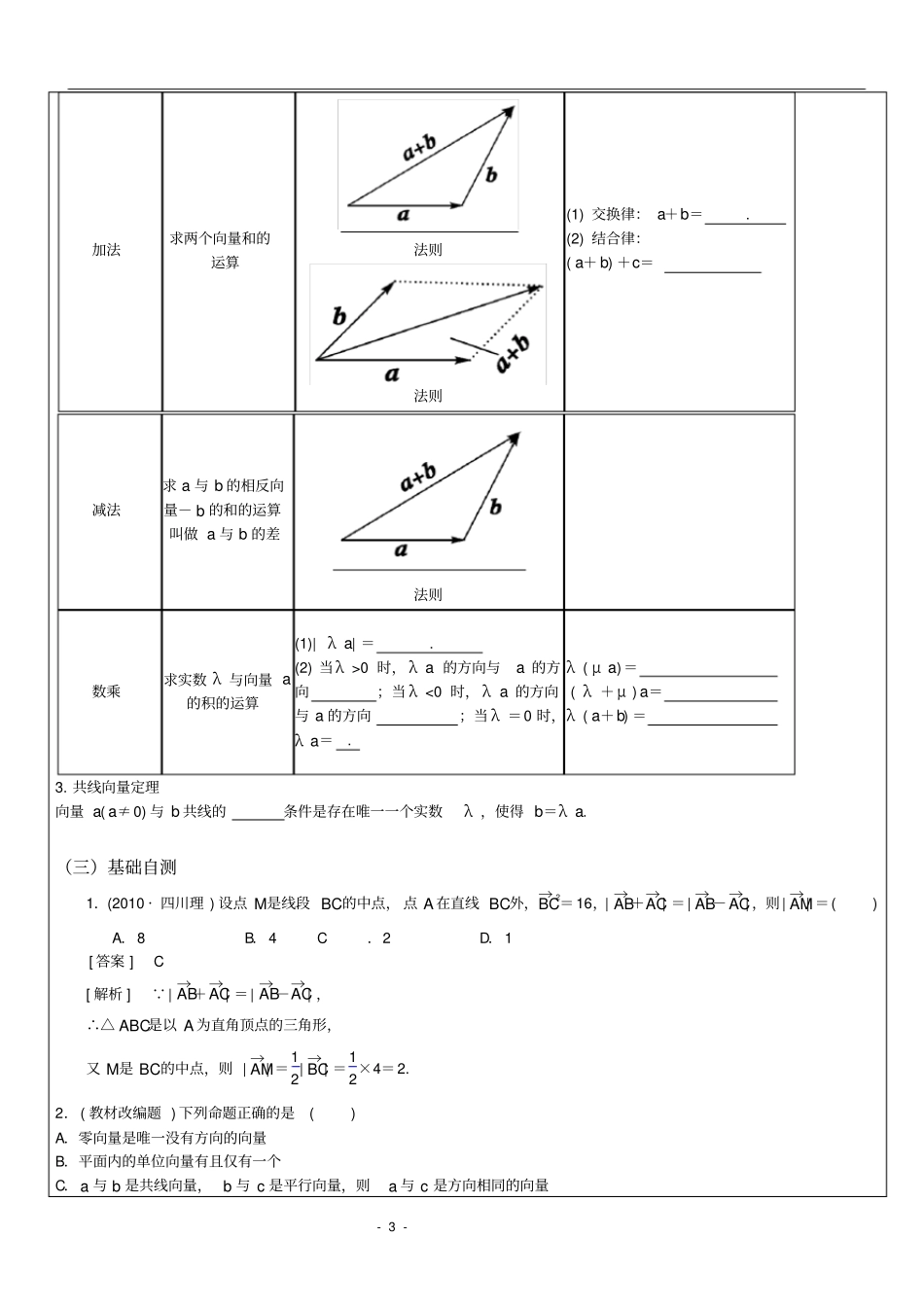
-1-年级:辅导科目:数学课时数:课题平面向量教学目的教学内容一、知识网络二、命题分析从近几年的高考可以看出,命题呈现以下特点:1.对于平面向量的基本概念及运算,将继续以选择题或填空题的形式单独考查,难度较低.2.重点考查向量的运算,向量的坐标运算和数量积为必考内容.-2-3.依然有可能出现以向量为工具,在二次曲线、不等式、三角恒等变换、解三角形等知识交汇点处命题的题目,而且综合性可能会加强,难度在中档以上.三、复习建议1.数形结合思想是向量加法、减法运算的核心.向量是一个几何量,是有“形”的量,因此在研究向量的有关问题时,一定要结合图形进行分析判断求解,这是研究平面向量最重要的方法与技巧.2.向量有几何法和坐标法两种表示形式,因此它的运算也有两种方式,故向量问题的解决有两种途径——几何法和代数法,在解决具体问题时要善于从不同的角度考虑问题.引入平面向量的坐标可以使向量运算完全代数化,成为数与形结合的载体;同时,增强数形转化的能力和培养运用运动变化的思想进行等价转化问题的能力,初步领会数学建模的思想和方法.3.数量积及其应用是本单元的重点和难点,只有对其定义及运算律理解透彻,才能准确灵活地运用.高考中主要考查判断两个向量是否垂直或是寻求两个向量垂直的条件,利用向量的数量积等条件求向量或向量的坐标.四、知识讲解第一节平面向量的概念及其线性运算(一)高考目标考纲解读1.了解向量的实际背景.2.理解平面向量的概念,理解两个向量相等的含义.3.理解向量的几何表示.4.掌握向量加法、减法的运算,并理解其几何意义.5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.6.了解向量线性运算的性质及其几何意义考向预测1.重点考查平面向量的有关概念、线性运算及其几何表示.2.多以选择题、填空题的形式呈现,常与解析几何相结合,在知识的交汇点处命题.3.向量是“形”与“数”的具体体现,注意数形结合思想的应用.(二)课前自主预习知识梳理1.向量的有关概念(1)向量:既有又有的量叫做向量,向量的大小叫做向量的(或模).(2)零向量:的向量叫做零向量,其方向是的.(3)单位向量:长度等于的向量.(4)平行向量:方向或的向量.平行向量又叫,任一组平行向量都可以移到同一条直线上.规定:0与任一向量.(5)相等向量:长度且方向的向量.(6)相反向量:长度且方向的向量.2.向量的线性运算向量运算定义法则(或几何意义)运算律-3-加法求两个向量和的运算法则法则(1)交换律:a+b=.(2)结合律:(a+b)+c=减法求a与b的相反向量-b的和的运算叫做a与b的差法则数乘求实数λ与向量a的积的运算(1)|λa|=.(2)当λ>0时,λa的方向与a的方向;当λ<0时,λa的方向与a的方向;当λ=0时,λa=.λ(μa)=(λ+μ)a=λ(a+b)=3.共线向量定理向量a(a≠0)与b共线的条件是存在唯一一个实数λ,使得b=λa.(三)基础自测1.(2010·四川理)设点M是线段BC的中点,点A在直线BC外,BC→2=16,|AB→+AC→|=|AB→-AC→|,则|AM→|=()A.8B.4C.2D.1[答案]C[解析] |AB→+AC→|=|AB→-AC→|,∴△ABC是以A为直角顶点的三角形,又M是BC的中点,则|AM→|=12|BC→|=12×4=2.2.(教材改编题)下列命题正确的是()A.零向量是唯一没有方向的向量B.平面内的单位向量有且仅有一个C.a与b是共线向量,b与c是平行向量,则a与c是方向相同的向量-4-D.相等的向量必是共线向量[答案]D[解析]向量是既有大小又有方向的量,所以零向量必有方向,又规定零向量与任一向量平行,所以零向量是唯一的一个方向不确定的向量,故A错误;对平面内的任一向量a而言,由于a|a|=1,所以a|a|即是一个单位向量,由a的任意性,可知B错误;共线向量即平行向量,包括方向相同或方向相反的非零向量及零向量,故C错误;由于相等向量即长度相等且方向相同的向量,所以D正确.3.(2009·湖南文)如图,D、E、F分别是△ABC的边AB、BC、CA的中点,则()A.AD→+BE→+CF→=0B.BD→-CF→+DF→=0C.AD→+CE→-CF→=0D.BD→-BE→-FC→=0[答案]A[解析]考查平面向量的线性运算.AD→+BE→+CF→=AD→+DF→+FA→=0....